Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-19T17:54:24.399Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementarfunktionen Auf Riemannschen Flächen Als Hilfsmittel Für Die Funktionentheorie MEHRERER Veränderlichen

Published online by Cambridge University Press:  20 November 2018

Heinrich Behnke  and
Karl Stein
Heinrich Behnke
Affiliation:
Münster (Westf.)
Karl Stein
Affiliation:
Münster (Westf.)
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the present paper, the authors extend the Cousin theorems and the continuity theorem, using some previous results on analytic functions connected with open Riemann surfaces.

The Cousin theorems, concerning the existence of analytic functions of several complex variables with prescribed poles and zeros in a given domain, have been generalized in various manners, but only in the case where the domain is schlicht. The authors proceed to the case where the given domain 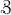is the direct product of n open Riemann surfaces. They prove the following two theorems.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 152 - 165
Copyright
Copyright © Canadian Mathematical Society 1950

References

1 Math. Ann., vol. 120 (1948).

2 Osgood, Siehe W. F., Lehrbuch der Funktionentheorie II,1,2. Auflage (1929), 248 ff.Google Scholar

3 Gronwall, T. H., “On the Expressibility of a Uniform Function of Several Complex Variables as the Quotient of Two Functions of Entire Character,” Trans. Amer. Math. Soc, vol. 18 (1917).Google Scholar

4 Siehe auch Herta Florack, Reguläre und meromorphe Funktionen auf nichtgeschlossenen Riemannschen Flächen, Dissertation, Münster 1948.

5 Behnke, Siehe H. and Thullen, P., Theorie der Funktionen mehrerer Komplexer Veränderlichen, Erg. d. Math. 3, 3 (y), abgekürzt B.-Th. Bericht.Google Scholar

6 Behnke, H., “Der Kontinuitätssatz und die Regulärkonvexität,” Math. Ann., vol. 11(1936), 392–397.Google Scholar

7 Kneser, H., “Der Satz von dem Fortbestehen der wesentlichen Singularity ten einer analytischen Funktion zweier Veranderlichen,” Jber. deutschen Math. Verein., vol. 41 (1932), 164 ff. ;Google Scholar und Ein Satz uber die Meromorphiebereiche analytischer Funktionen von mehreren Veranderlichen,” Math. Ann., vol. 106 (1932), 648 ff.

8 Herr W. Rothstein hat vor einigen Jahren schon einen andere Mittel benutzenden Beweis des verallgemeinerten Kontinuit'tssatzes fur meromorphe Funktionen vorgelegt, der wegen der besonderen Verh'ltnisse erst jetzt erscheinen konnte. Siehe W. Rothstein, “Die invariante Fassung des Kontinuit'tssatzes fur meromorphe Funktionen,”Archiv der Mathematik, vol. 1 (1948).

9 ist also das direkte Produkt von ℜ mit sich selbst. Durch die Schreibweise bzw. ℜz werde angedeutet, dass die Variable einmal , das andere Mal z heissen soil. Zur Kennzeichnung eines Punktes von . ℜz bzw. = ⨯ ℜzbenutzen wir die Symbole p() bzw. p(z) bzw. p(,z) = p() ⨯ p(z).

10 Wir sprechen von einem stùckweise glatten Kurvenstück, wenn es aus endlich vielen reell analytischen Kurvenstücken besteht.

11 Der Begriff des Integrals 1. Gattung auf einer offenen Riemannschen Fläche ist in manchen neueren Arbeiten enger gefasst worden. Siehe etwa Hornich, H., “Über transzendente Integrale erster Gattung,” Monatshefte Math.-Phys., vol. 47 (1939), 380 ff.Google Scholar

12 Siehe, , Behnke, , H. und Stein, K., “Analytische Funktionen mehrerer Veränderlichen zu vorgegebenen Null- und Polstellen,” Jber. Deutschen Math. Verein., vol. 47 (1937), 177–192.Google Scholar

13 Siehe B.- Th. Bericht, 25.

14 Vgl. H. Kneser, Math. Ann. 106, a.a.O.