Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T03:10:48.027Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenvalues of the Curvature Operator for Certain Homogeneous Manifolds

Published online by Cambridge University Press:  20 November 2018

J. E. D'Atri  and
I. Dotti Miatello
J. E. D'Atri
Affiliation:
Mathematics Department, Rutgers University, New Brunswick, N.J. 08903, USA
I. Dotti Miatello
Affiliation:
FAMAF, Universidad Nacional de Córdoba, Valparaiso y Rogelio Martinez, 5032 Cordoba, Argentina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a Riemannian manifold M, the Riemann tensor R induces the curvature operator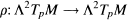 on the exterior power 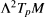of the tangent space, defined by the formula 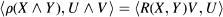where the inner product is defined by 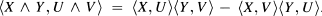From the symmetries of R, it follows that ρ is self-adjoint and so has only real eigenvalues. R also induces the sectional curvature function K on 2-planes in is 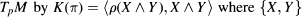an orthonormal basis of the 2-plane π.

Keywords

53C20 53C30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 6 , 01 December 1990 , pp. 981 - 999
Copyright
Copyright © Canadian Mathematical Society 1990

References

[A-W] Aloff, S. and Wallach, N.R., An infinite family of distinct 7-manifolds admitting positively curved Riemannian structures, Bull. A.M.S. 81 (1975), 93–97.Google Scholar
[B] Berger, M., Les variétés riemanniennes homogènes normales simplement convexes à courbure strictement positive, Ann. Scuola Norm. Sup. Pisa, 75 (1961), 179–246.Google Scholar
[Ch] Chavel, I., A class of riemannian homogeneous spaces, J. Diff. Geom. 4 (1970), 13–20.Google Scholar
[D'A] D'Atri, J., Quasi-symmetric is locally symmetric, J. Diff. Geom. 9 (1974), 275–277.Google Scholar
[D'A-Z] D'Atri, J.E. and Ziller, W., Naturually reductive metrics and Einstein metrics on compact Lie groups, Memoirs of the Am. Math. Soc, Vol. 18, Number 215, (1979).Google Scholar
[H] Heintze, E., On homogeneous manifolds of negative curvature, Math. Ann. 211 (1974), 23–34.Google Scholar
[He] Helgason, S., Differential geometry, Lie groups, and Symmetric spaces, Academic Press, New York, San Francisco, London 1978.Google Scholar
[Ki] Kostant, B., On differential geometry and homogeneous spaces 1, Proc. NAS, 42 (1956), 258–261.Google Scholar
[K2] Kostant, B., On differential geometry and homogeneous spaces II, Proc. NAS, 42 (1956), 354–357.Google Scholar
[K-NII] Kobayashi, S. and Nomizu, K., Foundations of differential geometry, Vol. II, Interscience, Wiley, New York (1969).Google Scholar
[M] Mostow, G.D., The extendability of local Lie groups of transformations and groups on surfaces, Ann. of Math. 52 (1950), 606–636.Google Scholar
[M-M] Micallef, M.J. and Moore, J.D., Minimal two-spheres and the topology of manifolds with positive curvature on totally isotropic two planes, Ann. of Math, 127 (1988), 199–227.Google Scholar
[Mo] Moore, J.D., Compact Riemannian manifolds with positive curvature operators, Bull. A.M.S. 14 (1986), 279–282.Google Scholar
[N] Nomizu, K., Studies on Riemannian homogeneous spaces, Nagoya Math. J. 9 (1955), 43–56.Google Scholar
[Si] Sagle, A., On anti-commutative algebras and homogeneous spaces, J. Math. Mech. 16 (1967), 1381–1394.Google Scholar
[S2] Sagle, A., A note on triple systems and totally geodesic submanifolds in a homogeneous space, Nagoya Math. J. 32 (1968), 5–20.Google Scholar
[Sa] Sampson, J.H., Applications of harmonic maps to Kähler geometry, Cont. Math. V. 49 (1986), 125-134.Google Scholar
[W] Wallach, N.R., Compact homogeneous Riemannian manifolds with strictly positive curvature, Ann. of Math. 96 (1972), 277–295.Google Scholar
[Wo] Wolf, J.A., Homogeneity and bounded isometries in manifolds of negative curvature, Illinois J. Math. 8 (1964), 14–18.Google Scholar