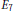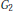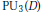Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gan, Wee Teck
2000.
An Automorphic Theta Module for Quaternionic Exceptional Groups.
Canadian Journal of Mathematics,
Vol. 52,
Issue. 4,
p.
737.
Savin, Gordan
and
Weissman, Martin H.
2011.
Dichotomy for generic supercuspidal representations ofG2.
Compositio Mathematica,
Vol. 147,
Issue. 3,
p.
735.
Gan, Wee Teck
and
Savin, Gordan
2023.
Howe duality and dichotomy for exceptional theta correspondences.
Inventiones mathematicae,
Vol. 232,
Issue. 1,
p.
1.
Bakić, Petar
and
Savin, Gordan
2024.
Howe duality for a quasi-split exceptional dual pair.
Mathematische Annalen,
Vol. 389,
Issue. 1,
p.
325.