Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:40:27.550Z Has data issue: false hasContentIssue false
  • English
  • Français

Domains of Paracompactness and Regularity

Published online by Cambridge University Press:  20 November 2018

S. MacDonald  and
S. Willard
S. MacDonald
Affiliation:
University of Maine, Portland-Gorham, Gorham, Maine
S. Willard
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a class 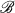of topological spaces and a class 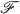of maps of topological spaces, our interest is in characterization of the class 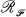(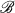) of topological spaces whose every 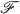-image lies in 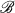. The class 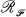(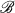) is referred to as the 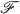-resolvent of 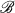and is the largest class of spaces smaller than 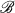closed under 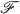-images (provided 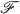is closed under composition and includes identity maps).

In the present paper, 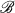will be either the class of paracompact spaces or the class of regular spaces, and the conditions determining 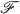will always include separation axioms on the range, some of which can be dispensed with now by agreeing that all spaces are Hausdorff.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 24 , Issue 6 , December 1972 , pp. 1079 - 1085
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Alexandroff, P. and Hopf, H., Topologie. I (Springer-Verlag Berlin, 1935).Google Scholar
2. Arens, R. and Dugundji, J., Remarks on the concept of compactness, Portugal. Math. 9 (1950), 141–143.Google Scholar
3. Dugundji, J., Topology (Allyn and Bacon, Boston, 1966).Google Scholar
4. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand, New York, 1960).Google Scholar
5. Katetov, M., On the equivalence of certain types of extensions of topological spaces, Časopis Pěst. Mat. 72 (1947), 101–106.Google Scholar
6. Stone, A. H., Paracompactness and product spaces, Bull. Amer. Math. Soc. 54 (1948), 977–982.Google Scholar
7. Willard, S., Metric spaces all of whose decompositions are metric, Proc. Amer. Math. Soc. 20 (1969), 126–128.Google Scholar