Article contents
Division Algebras of Prime Degree and Maximal Galois 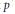 $p$-Extensions
$p$-Extensions
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 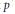 $p$ be an odd prime number, and let
$p$ be an odd prime number, and let 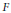 $F$ be a field of characteristic not
$F$ be a field of characteristic not 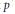 $p$ and not containing the group
$p$ and not containing the group 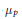 ${{\mu }_{p}}$ of
${{\mu }_{p}}$ of 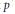 $p$-th roots of unity. We consider cyclic
$p$-th roots of unity. We consider cyclic 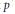 $p$-algebras over
$p$-algebras over 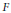 $F$ by descent from
$F$ by descent from 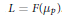 $L\,=\,F\left( {{\mu }_{p}} \right)$. We generalize a theorem of Albert by showing that if
$L\,=\,F\left( {{\mu }_{p}} \right)$. We generalize a theorem of Albert by showing that if 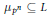 ${{\mu }_{{{p}^{n}}}}\,\subseteq \,L$, then a division algebra
${{\mu }_{{{p}^{n}}}}\,\subseteq \,L$, then a division algebra 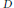 $D$ of degree
$D$ of degree 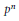 ${{p}^{n}}$ over
${{p}^{n}}$ over 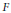 $F$ is a cyclic algebra if and only if there is
$F$ is a cyclic algebra if and only if there is 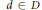 $d\,\in \,D$ with
$d\,\in \,D$ with 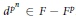 ${{d}^{{{P}^{n}}}}\,\in \,F\,-\,{{F}^{P}}$. Let
${{d}^{{{P}^{n}}}}\,\in \,F\,-\,{{F}^{P}}$. Let 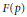 $F(p)$ be the maximal
$F(p)$ be the maximal 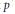 $p$-extension of
$p$-extension of 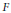 $F$. We show that
$F$. We show that 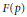 $F(p)$ has a noncyclic algebra of degree
$F(p)$ has a noncyclic algebra of degree 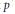 $p$ if and only if a certain eigencomponent of the
$p$ if and only if a certain eigencomponent of the 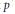 $p$-torsion of
$p$-torsion of 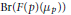 $\text{Br(F(p)(}{{\mu }_{p}}\text{))}$ is nontrivial. To get a better understanding of
$\text{Br(F(p)(}{{\mu }_{p}}\text{))}$ is nontrivial. To get a better understanding of 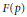 $F(p)$, we consider the valuations on
$F(p)$, we consider the valuations on 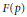 $F(p)$ with residue characteristic not
$F(p)$ with residue characteristic not 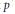 $p$, and determine what residue fields and value groups can occur. Our results support the conjecture that the
$p$, and determine what residue fields and value groups can occur. Our results support the conjecture that the 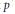 $p$ torsion in
$p$ torsion in 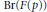 $\text{Br}(F(p))$ is always trivial.
$\text{Br}(F(p))$ is always trivial.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
- 1
- Cited by


