Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T17:30:00.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Divisibility of Direct Sums in Torsion Theories

Published online by Cambridge University Press:  20 November 2018

B. Sarath  and
K. Varadarajan
B. Sarath
Affiliation:
The University of Calgary, Calgary, Alberta
K. Varadarajan
Affiliation:
The University of Calgary, Calgary, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

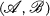Given a hereditary torsion theory on the category Mod 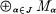R of right R-modules we obtain in this paper necessary and sufficient conditions for the direct sum of a given family 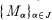of R-modules to be divisible for the torsion theory 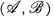. Using this criterion we show that if 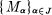is a family of R-modules having the property that 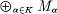is divisible for every countable subset 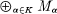K ol J then is itself divisible.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 1 , 01 February 1976 , pp. 211 - 214
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Bland, P. E., Divisible and codivisible modules, Math. Scand. 34 (1974), 153–161.Google Scholar
2. Dickson, S. E., A torsion theory for abelian categories, Trans. Amer. Math. Soc. 21 (1966), 223–235.Google Scholar
3. Lambek, J., Torsion theories, additive semantics, and rings of quotients, Lecture notes in Mathematics 177 (Springer-Verlag, 1971).Google Scholar
4. Sarath, B. and Varadarajan, K., Injectivity of direct sums, Comm. Algebra 1 (1974), 517–530.Google Scholar