Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T02:11:03.164Z Has data issue: false hasContentIssue false
  • English
  • Français

The Distribution of the First Elementary Divisor of the Reductions of a Generic Drinfeld Module of Arbitrary Rank

Published online by Cambridge University Press:  20 November 2018

Alina Carmen Cojocaru  and
Andrew Michael Shulman
Alina Carmen Cojocaru
Affiliation:
Department of Mathematics, Statistics and Computer Science, University of Illinois at Chicago, Chicago, 60607, IL, USA. email: [email protected] Institute of Mathematics "Simion Stoilow" of the Romanian Academy, Bucharest, 010702, Sector 1, Romania. email: [email protected]
Andrew Michael Shulman
Affiliation:
Department of Mathematics, Statistics and Computer Science, University of Illinois at Chicago, Chicago, 60607, IL, USA. email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 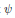$\psi$ be a generic Drinfeld module of rank 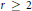$r\,\ge \,2$ . We study the first elementary divisor 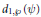${{d}_{1,\,\wp }}\,\left( \psi\right)$ of the reduction of 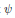$\psi$ modulo a prime $\wp $ , as $\wp $ varies. In particular, we prove the existence of the density of the primes $\wp $ for which 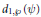${{d}_{1,\,\wp }}\,\left( \psi\right)$ is fixed. For 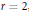$r\,=\,2$ , we also study the second elementary divisor (the exponent) of the reduction of 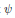$\psi$ modulo $\wp $ and prove that, on average, it has a large norm. Our work is motivated by J.-P. Serre's study of an elliptic curve analogue of Artin's Primitive Root Conjecture, and, moreover, by refinements to Serre's study developed by the first author and M. R. Murty.

Keywords

11R4511G0911R58Drinfeld modulesdensity theorems
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 6 , 01 December 2015 , pp. 1326 - 1357
Copyright
Copyright © Canadian Mathematical Society 2015

References

[Br] Breuer, F., Torsion bounds for elliptic curves and Drinfeld modules. J. Number Theory 130(2010), no. 5, 1241–1250. http://dx.doi.org/10.1016/j.jnt.2009.11.009 Google Scholar
[Co1] Cojocaru, A. C., On the cyclicity of the group of -rational points of non-CM elliptic curves. J. Number Theory 96(2002), no. 2, 335–350.Google Scholar
[Co2] Cojocaru, A. C., Cyclicity of CM elliptic curves modulo p. Trans. Amer. Math. Soc. 355(2003), no. 7, 2651–2662.http://dx.doi.org/10.1090/S0002-9947-03-03283-5 Google Scholar
[Co3] Cojocaru, A. C., Questions about the reductions modulo primes of an elliptic curve. In: Number theory, CRM Proc. Lecture Notes, 36, American Mathematical Society, Providence, RI, 2004, pp. 61–79.Google Scholar
[CoMu] Cojocaru, A. C. and Murty, M. R., Cyclicity of elliptic curves modulo p and elliptic curve analogues of Linnik's problem. Math. Ann. 330(2004), no. 3, 601–625.http://dx.doi.org/10.1007/s00208-004-0562-x Google Scholar
[CoPa] Cojocaru, A. C. and Papikian, M., Drinfeld modules, Frobenius endomorphisms, and CM liftings. Int. Math. Res. Notices (2014). http://dx.doi.org/10.1093/imrn/rnu178 Google Scholar
[CoSh] Cojocaru, A. C. and Shulman, A. M., An average Chebotarev density theorem for generic rank 2 Drinfeld modules with complex multiplication. J. Number Theory 133(2013), no. 3, 897–914.http://dx.doi.org/10.1016/j.jnt.2012.07.001 Google Scholar
[CoTo] Cojocaru, A. C. and Tóth, Á., The distribution and growth of the elementary divisors of the reductions of an elliptic curve over a function field. J. Number Theory 132(2012), no. 5, 953–965.http://dx.doi.org/10.1016/j.jnt.2011.08.007 Google Scholar
[Du] Duke, W., Almost all reductions modulo p of an elliptic curve have large exponent. C. R. Acad. Sci. Paris 337(2003), no. 11, 689–692.http://dx.doi.org/10.1016/j.crma.2003.10.006 Google Scholar
[FrKu] Freiberg, T. and Kurlberg, P., On the average exponent of elliptic curves modulo p. Int. Math. Res. Not. IMRN 2014, no. 8, 2265–2293.Google Scholar
[Ga] Gardeyn, F., Une borne pour l'action de l'inertie sauvage sur la torsion d'un module de Drinfeld. Arch. Math. 79(2002), no. 4, 241–251.http://dx.doi.org/10.1007/s00013-002-8310-5 Google Scholar
[Ge] Gekeler, E.-U., On finite Drinfel'd modules. J. Algebra 141(1991), no. 1, 187–203.http://dx.doi.org/10.1016/0021-8693(91)90211-P Google Scholar
[Go] Goss, D., Basic structures of function field arithmetic. Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 35, Springer-Verlag, Berlin, 1996.Google Scholar
[Ha] Hayes, D. R., Explicit class field theory in global function fields. In: Studies in algebra and number theory, Adv. in Math. Suppl. Stud., 6, Academic Press, New York-London, 1979, pp. 173–217.Google Scholar
[He] van der Heiden, G.-J., Weil pairing for Drinfeld modules. Monatsh. Math. 143(2004), no. 2, 115–143.http://dx.doi.org/10.1007/s00605-004-0261-4 Google Scholar
[Ki] Kim, Sungjin, Average behaviors of invariant factors in Mordell-Weil groups of CM elliptic curves modulo p. Finite Fields Appl. 30(2014), 178–190.http://dx.doi.org/10.1016/j.ffa.2014.07.003 Google Scholar
[KuLi] Kuo, W. and Liu, Y.-R., Cyclicity of finite Drinfeld modules. J. Lond. Math. Soc. (2) 80(2009), no. 3, 567–584.http://dx.doi.org/10.1112/jlms/jdp043 Google Scholar
[La] Lang, S., Algebra. Third ed., Graduate Texts in Mathematics, 211, Spring-Verlag, New York, 2002.Google Scholar
[Mu] Murty, M. R., On Artin's conjecture. J. Number Theory 16(1983), no. 2, 147–168.http://dx.doi.org/10.1016/0022-314X(83)90039-2 Google Scholar
[MuSc] Murty, V. K. and Scherk, J., Effective versions of the Chebotarev density theorem for function fields. C. R. Acad. Sci. Paris Sér. I 319(1994), no. 6, 523–528.Google Scholar
[Pi] Pink, R., The Mumford-Tate conjecture for Drinfeld modules. Publ. Res. Inst. Math. Sci. 33(1997), no. 3, 393–425.http://dx.doi.org/10.2977/prims/1195145322 Google Scholar
[PiRu] Pink, R. and Rütsche, E., Adelic openness for Drinfeld modules in generic characteristic. J. Number Theory 129(2009), no. 4, 882–907.http://dx.doi.org/10.1016/j.jnt.2008.12.002 Google Scholar
[Ro] Rosen, M., Number theory in function fields. Graduate Texts in Mathematics, 210, Springer-Verlag, New York, 2002.Google Scholar
[Sc] Schoof, R., The exponents of the groups of points on the reductions of an elliptic curve. In: Arithmetic algebraic geometry (Texel, 1989), Prog. Math., 89, Birkhäuser Boston, Boston, MA, 1991, pp. 325–335.Google Scholar
[Se] Serre, J-P., Summaries of courses of the 1977-78 academic year. (French), Collège de France, Paris, 1978, pp. 67–71.Google Scholar
[Tag1] Taguchi, Y., The Tate conjecture for t-motives. Proc. Amer. Math. Soc. 123(1995), no. 11, 3285–3287.Google Scholar
[Tag2] Taguchi, Y., On Ф-modules. J. Number Theory 60(1996), no. 1, 124–411.http://dx.doi.org/10.1006/jnth.1996.0117 Google Scholar
[Tak] Taguchi, Y., Good reduction of elliptic modules. J. Math. Soc. Japan 34(1982), no. 3, 475–487.http://dx.doi.org/10.2969/jmsj/03430475 Google Scholar
[Th] Thakur, D., Function field arithmetic. World Scientific Publishing Co. Inc., River Edge, NJ, 2004.Google Scholar
[Wu] Wu, J., The average exponent of elliptic curves modulo p. J. Number Theory 135(2014), 28–35.http://dx.doi.org/10.1016/j.jnt.2013.08.009 Google Scholar