Published online by Cambridge University Press: 20 November 2018
Let L be a finitely generated extension of a field K of characteristic p ≠ 0. If L/K is algebraic, then there is a unique intermediate field S such that
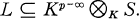
S is just the maximal separable extension of K in L. If L/K is not algebraic, then Dieudonne [4] showed there exist maximal separable extensions D of K in L such that L ⊆ Kp–∞⊗KD. In general, not every maximal separable extension of K in L has the property. Those which do have the property are called distinguished. Kraft [7] established that a maximal separable extension D of K in L is distinguished if and only if [L:D] is as small as possible. If the minimum of the [L:D] is pr, r is called the order of inseparability of L/K, denoted inor (L/K).
Let L1 be an intermediate field of L/K. If L/K is algebraic, then the maximal separable extension S1 of K in L1 is contained in the maximal separable extension S of K in L, and moreover S is separable over S1.