Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:37:53.058Z Has data issue: false hasContentIssue false
  • English
  • Français

Disjointly Additive Operators and Modular Spaces

Published online by Cambridge University Press:  20 November 2018

Iwo Labuda
Iwo Labuda*
Affiliation:
Department of Mathematics Kuwait UniversityP.O. Box 5969 Kuwait 13060
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By now the literature concerning the representation of disjointly additive functionals and operators is quite extensive. A few entries on the subject are [6, 7, 8, 11, 20, 21]. In [7, 8, 17] further references can be found, in [7] the “prehistory” of the subject is also discussed.

To quote a typical result, we may take a 1967 theorem of Drewnowski and Orlicz ([6] Th. 3.2, [17] 12.4) which asserts that, under proper assumptions, an abstract modular (= disjointly countably additive functional) p on a “substantial“ subspace D of L° can be realized by the formula .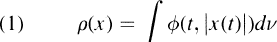

Keywords

47H9946A9946E30Disjointly additive nonlinear operatormodular spaceAbramovich extension
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 3 , 01 June 1990 , pp. 508 - 519
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Abramovich, Y., On the maximal normed extension of partially ordered normed spaces, Vestnik Leningrad. Univ. 26 No. 1 (197), 7-17; or English transi., in Vestnik Leningrad Univ. Math 3 (1976), 1–12.Google Scholar
2. Aliprantis, C., Burkinshaw, O., Locally solid Riesz spaces, New York, Academic Press, 1978.Google Scholar
3. Aronszajn, N., Szeptycki, P., On general integral transformations, Math. Ann. 163 (1966), 127- 154.Google Scholar
4. Bourbaki, N., General Topology, Hermann-Addison-Wesley Co., 1966.Google Scholar
5. Drewnowski, L., Un théorème sur les operateurs de, l∞(Γ) C.R. Acad. Sci. Paris 281 (1975), 967–969.Google Scholar
6. Drewnowski, L., Orlicz, W., A note on modular spaces, X, Bull. Acad. Polon. Sci., Ser. Sci. Math. Astronom. Phys., 16 (1968), 809–814.Google Scholar
7. Drewnowski, L., Orlicz, W., Continuity and representation of orthogonally additive functional, ibidem, 77 (1969), 647–653.Google Scholar
8. Friedman, N.A., Tong, A.E., On additive operators, Canadian J. Math. 23 (3) (1971), 468–480.Google Scholar
9. Kantorovich, L., Akilov, G., Functional Analysis (2nd Edition), Oxford, Pergamon Press, 1982.Google Scholar
10. Kalton, N.J., Exhaustive operators and vector measures, Proc. Edinburgh Math. Soc. II Ser. 19 (1975), 291–300.Google Scholar
11. Kozlowski, W., On domains of some nonlinear operators, J. Math. Anal. Appl. J39(1), 1989, 243–267.Google Scholar
12. Labuda, I., Completeness type properties of locally solid Riesz spaces, Studia Math., 77 (1984), 349–372.Google Scholar
13. Labuda, I., On the largest o-enlargement of a locally solid Riesz space, Bull. Pol. Acad. Math., 33 (1985), 615–622.Google Scholar
14. Labuda, I., Submeasures and locally solid topologies on Riesz spaces, Math. Z., 195 (1987), 179–196.Google Scholar
15. Labuda, I., Szeptycki, P., Extensions of integral operators, Math. Ann., 281 (1988), 341–353.Google Scholar
16. Leśniewicz, R., Orlicz, W., A note on modular spaces, XIV, Bull. Acad. Pol. Sci., Sér. Sci. Math. Astronom. Phys., 22(9) (1974), 915–923.Google Scholar
17. Musielak, J., Orlicz spaces and modular spaces, Lecture Notes in Mathematics 1034, Springer Verlag 1983.Google Scholar
18. Rolewicz, S., Metric Linear Spaces, D. Reidel Publishing Co. 1985.Google Scholar
19. Szeptycki, P., Notes on integral transformations, Dissertationes Math., 231 (1984), 1–52.Google Scholar
20. Woyczyński, W.A., Additive functional on Orlicz spaces, Colloq. Math., 19 (1968), 319–326.Google Scholar
21. Woyczyński, W.A., Additive operators, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys., 77 (1969), 447–51.Google Scholar
22. Zaanen, A.C., Integration, Amsterdam, North Holland, 1967.Google Scholar