Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T01:31:30.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrete Subsets of Proximity Spaces

Published online by Cambridge University Press:  20 November 2018

Don A. Mattson
Don A. Mattson*
Affiliation:
Moorhead State University, Moorhead, Minnesota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The distinct Hausdorff compactifications δX of a completely regular (Hausdorff) space X are in one-one correspondence with the admissible proximity relations δ on X, or alternatively, with the admissible totally bounded uniform structures for X. (See [1], [2].) Thus, δX is the Smirnov compactification of (X, δ). Generalized uniform structures 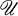for X will be described by means of pseudometrics on X (cf. [5], [7], [13]). Let 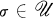where 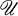is in the proximity class π(δ) associated with (X, δ). Then a subset S of X is σ-discrete of gauge 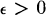if , for all x, y ∈ S where x ≠ y.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 2 , 01 April 1979 , pp. 225 - 230
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Alfsen, E. M. and Fenstad, J. E., A note on completion and compactification, Math. Scand. 8 (1960), 97–104.Google Scholar
2. Alfsen, E. M. and Njastad, O., Proximity and generalized uniformity, Fund. Math. 52 (1963), 235–252.Google Scholar
3. Chandler, R. E. and Cellar, R., The compactifications to which an element of C*(X) extends, Proc. Amer. Math. Soc. 38 (1973), 637–639.Google Scholar
4. Gantner, T., Extensions of uniformly continuous pseudometrics, Trans. Amer. Math. Soc. 132 (1968), 147–157.Google Scholar
5. Gillman, L. and Jerison, M., Rings of continuous functions, (The University Series in Higher Math., Princeton, N.J., 1960).Google Scholar
6. Harris, D., An internal characterization of realcompactness, Can. J. Math. 23 (1971), 439–444.Google Scholar
7. Leader, S., On pseudometrics for generalized uniform structures, Proc. Amer. Math. Soc. 16 (1965), 493–495.Google Scholar
8. Mattson, D., Real maximal round filters in proximity spaces, Fund. Math. 78 (1973), 183–188.Google Scholar
9. Mattson, D., On completions of proximity and uniform spaces, Coll. Math. 38 (1977), 55–62.Google Scholar
10. Njastad, O., On p-systems and p-functions, Norske Vid. Selsk. Skr. 1 (1968), 1–10.Google Scholar
11. Njastad, O., On real-valued proximity mappings, Math. Annale. 154 (1964), 413–419.Google Scholar
12. Reed, E. E. and Thron, W. J., n-bounded uniformities, Trans. Amer. Math. Soc. 141 (1969), 71–77.Google Scholar
13. Thron, W. S., Topological structures, (Holt, Rinehart, and Winston, New York, 1966).Google Scholar