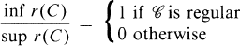Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rodin, Burt
1987.
Schwarz's lemma for circle packings.
Inventiones Mathematicae,
Vol. 89,
Issue. 2,
p.
271.
Rodin, Burt
and
Sullivan, Dennis
1987.
The convergence of circle packings to the Riemann mapping.
Journal of Differential Geometry,
Vol. 26,
Issue. 2,
Pach, J.
1989.
Delicate symmetry.
Computers & Mathematics with Applications,
Vol. 17,
Issue. 1-3,
p.
117.
Fejes Tóth, L.
1989.
Research problems.
Periodica Mathematica Hungarica,
Vol. 20,
Issue. 1,
p.
89.
PACH, J.
1989.
Symmetry 2.
p.
117.
Schramm, Oded
1991.
Rigidity of infinite (circle) packings.
Journal of the American Mathematical Society,
Vol. 4,
Issue. 1,
p.
127.
Carter, Ithiel
and
Rodin, Burt
1992.
An inverse problem for circle packing and conformal mapping.
Transactions of the American Mathematical Society,
Vol. 334,
Issue. 2,
p.
861.
TÖTH, Gábor FEJES
and
KUPERBERG, Wlodzimierz
1993.
Handbook of Convex Geometry.
p.
799.
Tóth, Gábor Fejes
and
Kuperberg, Wlodzimierz
1993.
New Trends in Discrete and Computational Geometry.
Vol. 10,
Issue. ,
p.
251.
Doyle, P.
He, Zheng-Xu
and
Rodin, B.
1994.
The asymptotic value of the circle-packing rigidity constants s n *.
Discrete & Computational Geometry,
Vol. 12,
Issue. 1,
p.
105.
Dubejko, Tomasz
1995.
Branched circle packings and discrete Blaschke products.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 10,
p.
4073.
1995.
Combinatorial Geometry.
p.
319.
Huang, Xiaojun
and
Shen, Liang
2009.
On the convergence of circle packings to the quasiconformal map.
Acta Mathematica Scientia,
Vol. 29,
Issue. 5,
p.
1173.
Schramm, Oded
2011.
Selected Works of Oded Schramm.
p.
63.
Peretz, Ronen
2012.
The Discontinuity Function of Discrete Groups and Radius of Schlichtness.
Complex Analysis and Operator Theory,
Vol. 6,
Issue. 6,
p.
1189.
 of openly disjoint discs in the plane
is said to form a 6-neighboured circle packing if every
of openly disjoint discs in the plane
is said to form a 6-neighboured circle packing if every  is tangent to at least 6 other elements of
is tangent to at least 6 other elements of 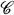 (It is evident that such a system consists of infinitely many discs.) The simplest example is the regular circle packing all of whose circles are of the same size and have exactly 6 neighbours. L. Fejes Tóth conjectured that the regular circle packing has the interesting extremal property that, if we slightly “perturb” it, then there will necessarily occur either arbitrarily small or arbitrarily large circles. More precisely, he asked whether or not the following “zero or one law” (cf. [3], [6]) is valid: If
(It is evident that such a system consists of infinitely many discs.) The simplest example is the regular circle packing all of whose circles are of the same size and have exactly 6 neighbours. L. Fejes Tóth conjectured that the regular circle packing has the interesting extremal property that, if we slightly “perturb” it, then there will necessarily occur either arbitrarily small or arbitrarily large circles. More precisely, he asked whether or not the following “zero or one law” (cf. [3], [6]) is valid: If 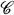 is a 6-neighboured circle packing, then
is a 6-neighboured circle packing, then