Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:40:48.319Z Has data issue: false hasContentIssue false
  • English
  • Français

The Dirichlet Problem for the Subelliptic Laplacian on the Heisenberg Group II

Published online by Cambridge University Press:  20 November 2018

Bernard Gaveau  and
Jacques Vauthier
Bernard Gaveau
Affiliation:
Université Pierre et Marie Curie, Paris, France
Jacques Vauthier
Affiliation:
Université Pierre et Marie Curie, Paris, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H3 be the Heisenberg group in three dimensions, Δ the fundamental subelliptic laplacian on H3 (see Section 1 for notations and definitions) and U be an open subset of H3 If φ is a continuous function on the boundary ∂U of U, the Dirichlet problem is thus,

(1)

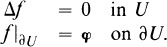
In [3], p. 104, it was asserted by the first author that, when dU is regular (see Section 1 for this definition), the problem (1) has a solution continuous on D and a probabilistic formula was given. In [3], we prove that our probabilistic formula gives a solution of the so called “martingale problem” associated to Δ on U (see [5] for this notion). But it appears that the connection between the solution in the martingale problem sense and the true solution is not at all clear in the subelliptic case; in particular it is not obvious at all that the probabilistic formula is a C2 function.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 4 , 01 August 1985 , pp. 760 - 766
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Bony, J. M., Opérateurs elliptiques dégénérés associés aux axiomatiques de la théorie du potentiel, Cours au CIME (1969), Edizioni Cremonese Roma (1970).Google Scholar
2. Courant, R. and Hilbert, D., Mathematical physics, Vol 2 (Interscience, 1965).Google Scholar
3. Gaveau, B., Principe de moindre action, propagation de la chaleur et estimées sous-elliptiques sur certains groupes nilpotents, Acta Mathematica 139 (1977), 96–153.Google Scholar
4. Gaveau, B., Greiner, P. and Vauthier, J., Polynômes harmoniques et groupe d'Heisenberg, Bulletin des Sciences Mathématiques 2e série, 108 (1984), 337–354.Google Scholar
5. Stroock, D. and Varadhan, S., Diffusion processes with continuous coefficients, Communication in Pure and Applied Mathematics 22 (1969), 345–400.Google Scholar