Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:56:16.053Z Has data issue: false hasContentIssue false
  • English
  • Français

Directed Graphs and the Jacobi-Trudi Identity

Published online by Cambridge University Press:  20 November 2018

I. P. Goulden
I. P. Goulden*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let |aij|n×n denote the n × n determinant with (i, j)-entry aij, and hk = hk(x1, …, xn) denote the kth-homogeneous symmetric function of x1, …, xn defined by

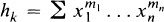
where the summation is over all m1, …, mn ≧ 0 such that m1 + … + mn = k. We adopt the convention that hk = 0 for k < 0. For integers α1 ≧ α2 … ≧ αn ≧ 0, the Jacobi-Trudi identity (see [6], [7]) states that

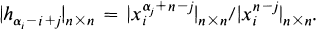
In this paper we give a combinatorial proof of an equivalent identity, Theorem 1.1, obtained by moving the denominator on the RHS to the numerator on the LHS.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 6 , 01 December 1985 , pp. 1201 - 1210
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Bressoud, D. M., Colored tournaments and Weyl's denominator formula, preprint.Google Scholar
2. Bressoud, D. M. and Goulden, I. P., Constant term identities extending the q-Dyson theorem, Trans. Amer. Math. Soc. (to appear).Google Scholar
3. Gessel, I., Tournaments and Vandermonde's determinant, J. Graph Theory 3 (1979), 305–307.Google Scholar
4. Gessel, I. and Viennot, G., Determinants and plane partition, preprint.Google Scholar
5. Goulden, I. P. and Jackson, D. M., Combinatorial enumeration (J. Wiley, New York, 1983).Google Scholar
6. Macdonald, I. G., Symmetric functions and Hall polynomials (Clarendon Press, Oxford, 1979).Google Scholar
7. Stanley, R. P., Theory and applications of plane partitions: Parts I and II, Studies in applied mathematics 50 (1971), 167–188; 259–279.Google Scholar
8. Zeilberger, D. and Bressoud, D. M., A proof of Andrews’ q-Dyson conjecture, Discrete Math. 54 (1985), 201–224.Google Scholar