Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T16:17:52.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Directed Covers and Paracompact Spaces

Published online by Cambridge University Press:  20 November 2018

John Mack
John Mack*
Affiliation:
University of Kentucky
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

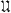A cover is directed (is well-ordered, totally ordered) if it is directed (is well-ordered, totally ordered, respectively) by set inclusion. Specifically 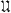is directed if, given U, V in 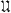, there exists W in 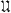such that U ⋃ V ⊂ W.

Directed covers have been used implicitly in numerous theorems dealing with paracompactness and related properties. In particular, characterizations of paracompactness in terms of product spaces seem to require the use of directed covers (3; 11, §2; or 12). However, the utility of directed covers has not been fully exploited.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 649 - 654
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Alexandroff, P. and Urysohn, P., Mémoire sur les espaces topologiques compactes, Verh. Nederl. Akad. Wetensch. (Amsterdam), 14 (1929), 1–96.Google Scholar
2. Arens, R. and Dugundi, J., Remark on the concept of compactness, Portugal. Math., 9 (1950), 141–143.Google Scholar
3. Dowker, C. H., On countably paracompact spaces, Can. J. Math., 8 (1951), 219–224.Google Scholar
4. Iséki, K. and Kasahara, S., On pseudo-compact and countably compact spaces, Proc. Japan Acad., 33 (1957), 100–102.Google Scholar
5. Ishikawa, F., On countably paracompact spaces, Proc. Japan Acad., 31 (1955), 686–687.Google Scholar
6. Mack, John, On a class of countably paracompact spaces, Proc. Amer. Math. Soc., 16 (1965), 467–472.Google Scholar
7. Michael, E., A note on paracompact spaces, Proc. Amer. Math. Soc., 4 (1953), 831–838.Google Scholar
8. Michael, E., Another note on paracompact spaces, Proc. Amer. Math. Soc., 8 (1957), 822–828.Google Scholar
9. Michael, E., Yet another note on paracompact spaces, Proc. Amer. Math. Soc., 10 (1959), 309–314.Google Scholar
10. Michael, E., Point-finite and locally finite coverings, Can. J. Math., 7 (1955), 275–279.Google Scholar
11. Morita, K., Paracompactness and product spaces, Fund. Math., 50 (1961), 223–236.Google Scholar
12. Tamano, H., On paracompact spaces, Pacific J. Math., 10 (1960), 1043–1047.Google Scholar