Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-16T15:05:57.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirac Systems with Discrete Spectra

Published online by Cambridge University Press:  20 November 2018

D. B. Hinton  and
J. K. Shaw
D. B. Hinton
Affiliation:
University of Tennessee, Knoxville, Tennessee
J. K. Shaw
Affiliation:
Virginia Tech, Blacksburg, Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the one dimensional Dirac system

1.1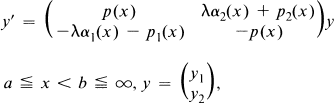

where αk(x) < 0, λ is a complex spectral parameter, and the remaining coefficients are suitably smooth and real valued. We regard (1.1) as regular at x = a but singular at x = b; in Section 4 we extend our result to problems having two singular endpoints.

Equation (1.1) arises from the three dimensional Dirac equation with spherically symmetric potential, following a separation of variables. For the choices p(x) = k/x, αk(x) = 1,p2(x) = (z/x) + c, p1(x) = (z/x) – c, and appropriate values of the constants, (1.1) is the radial wave equation in relativistic quantum mechanics for a particle in a field of potential V = z/x [17]. Such an equation was studied by Kalf [11] in the context of limit point-limit circle criteria, which is one of the matters we consider here.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 1 , 01 February 1987 , pp. 100 - 122
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Barut, A. O. and Kraus, J., Solution of the Dirac equation with Coulomb and magnetic moment reactions, J. Math. Phys. 17 (1976), 506–508.Google Scholar
2. Coppel, W. A., Stability and asymptotic behavior of differential equations, (D.C. Heath, Boston, 1965).Google Scholar
3. Hinton, D. B., Asymptotic behavior of solutions of disconjugate differential equations, in Differential equations, (North-Holland, Amsterdam, 1984), 293–300.Google Scholar
4. Hinton, D. B. and Shaw, J. K., On Titchmarsh-Weyl m-functions for linear Hamiltonian systems, J. Diff. Eqs. 40(1981), 316–342.Google Scholar
5. Hinton, D. B. and Shaw, J. K., Hamiltonian systems of limit point or limit circle type with both endpoints singular, J. Diff. Eqs. 50 (1983), 444–464.Google Scholar
6. Hinton, D. B. and Shaw, J. K., On the spectrum of a singular Hamiltonian system, Quaestiones Math. 5 (1982), 29–81.Google Scholar
7. Hinton, D. B. and Shaw, J. K., On the spectrum of a singular Hamiltonian system II, Quaestiones Math. 10 (1986), 1–48.Google Scholar
8. Hinton, D. B. and Shaw, J. K., Absolutely continuous spectra of Dirac systems with long range, short range and oscillating potentials, Quart. J. Math. Oxford (2), 36 (1985), 183–213.Google Scholar
9. Hinton, D. B. and Shaw, J. K., Some extensions of results of Titchmarsh on Dirac systems, Proceedings of the 1984 Workshop on Spectral Theory of Sturm-Liouville Differential Operators, Argonne National Laboratory Technical Report No. ANL-84-73, (1984), 135–144.Google Scholar
10. Hinton, D. B. and Shaw, J. K., Parameterization of the m-function for a Hamiltonian system of limit circle type, Proc. Roy. Soc. Edinburgh Sect. A93, (1983), 349–360.Google Scholar
11. Kalf, H., A limit point criterion for separated Dirac operators and a little known result on Riccat's equation, Math. Zeit. 129 (1972), 75–82.Google Scholar
12. Kogan, V. I. and Rofe-Beketov, F. S., On square-integrable solutions of symmetric systems of differential equations of arbitrary order, Proc. Roy Soc. Edin. Sec. A74, (1974), 5–40.Google Scholar
13. Levitan, B. M. and Sarqsjan, I. S., Introduction to spectral theory: self adjoint ordinary differential operators, Translations of Mathematical Monographs 39 (American Mathematical Society, Providence, R.I., 1975).Google Scholar
14. Read, T. T., A limit point criterion for expressions with intermittently positive coefficients, J. London Math. Soc. (2) 15 (1977), 271–276.Google Scholar
15. Roos, B. W. and Sangren, W. C., Spectra for a pair of singular first order differential equations, Proc. Amer. Math. Soc. 12 (1961), 468–476.Google Scholar
16. Stone, M. H., Linear transformations in Hilbert space and their applications to analysis, Am. Math. Soc. Colloq. Publications 75 (Am. Math. Soc, Providence, R.I., 1932).Google Scholar
17. Titchmarsh, E. C., On the relation between the eigenvalues in relativistic and nonrelativistic quantum mechanics, Proc. Roy. Soc. A266 (1962), 33–46.Google Scholar
18. Titchmarsh, E. C., On the nature of the spectrum in problems of relativistic quantum mechanics, Quart. J. Math. Oxford (2) 12 (1961), 227–240.Google Scholar
19. Titchmarsh, E. C., On the nature of the spectrum in problems of relativistic quantum mechanics III, Quart. J. Math. Oxford (2) 13 (1962), 255–263.Google Scholar
20. Titchmarsh, E. C., Eigenfunction expansions associated with second order differential equations, Part 1, 2nd ed. (Oxford Univ. Press, Oxford, 1962).Google Scholar
21. Weidmann, J., Oszillationsmethoden fur système gewohnlicher differentialgleichungen, Math. Zeit. 119 (1971), 349–373.Google Scholar