Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T22:04:49.207Z Has data issue: false hasContentIssue false
  • English
  • Français

A Dimension Theorem for Real Primes

Published online by Cambridge University Press:  20 November 2018

D. Dubois  and
G. Efroymson
D. Dubois
Affiliation:
University of New Mexico, Albuquerque, New Mexico
G. Efroymson
Affiliation:
University of New Mexico, Albuquerque, New Mexico
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be a real closed field (see § 2 for a definition). Let 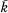be an algebraic closure of k. An algebraic set denned over k is, as usual, a subset of 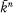(n some integer greater than 0) which is the set of zeros of some polynomials in k[X1, . . . , Xn]. A variety is denned to be an absolutely irreducible algebraic set. We define the real points of an algebraic set X to be the points in X ∩ kn. One can then define X to be real if I(X ∩ kn) = I(X). (I(X) = the polynomials in k[X1, . . . , Xn] which vanish on X.)

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 1 , February 1974 , pp. 108 - 114
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Dubois, D., A nullstellensatz for ordered fields, Ark. Mat. 8 (1967), 111–114.Google Scholar
2. Dubois, D., A Grothendieck with the collaboration of J. Dieudonné, Elements de Géométrie Algébrique, I.H.E.S., Bures sur Yvette.Google Scholar
3. Grothendieck, A., Local properties of morphisms, a course given at Harvard University, 1963.Google Scholar
4. Jacobson, N., Lectures in abstract algebra, Volume III, Theory of fields and Galois theory (D. Van Nostrand Co. Inc., Princeton University Press, 1964).Google Scholar
5. Nakai, Y. and Nishimura, H., On the existence of a curve connecting given points on an abstract variety, Mem. Coll. Sci., Kyoto, Series A, Vol. XXVIII, Math. No. 8 (1954), 267–270.Google Scholar
6. Zariski, O., Introduction to the problem of minimal models in the theory of algebraic surfaces, Japan J. Math. (1958).Google Scholar