Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:03:25.114Z Has data issue: false hasContentIssue false
  • English
  • Français

A Difference-Differential Basis Theorem

Published online by Cambridge University Press:  20 November 2018

Richard M. Cohn
Richard M. Cohn*
Affiliation:
Rutgers University, New Brunswick, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our aim in this paper is to extend to difference-differential rings the beautiful theorem of Kolchin [5, Theorem 3] for the differential case. The necessity portion of Kolchin's result is not obtained.

What might well be called the Ritt basis theorem states that if a commutative ring R with identity is finitely generated over a subring R0, then the ascending chain condition for radical ideals of R0 implies the ascending chain condition for radical ideals of R. (This is indeed a basis theorem. If we define a basis for a radical ideal A to be a finite set B such that 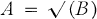then every radical ideal of a ring R has a basis if and only if the ascending chain condition for radical ideals holds in R.) It is the Ritt basis theorem rather than the Hilbert basis theorem which has appropriate generalizations in differential and difference algebra, where in fact it originated.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 6 , 01 December 1970 , pp. 1224 - 1237
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Cohn, R. M., Difference algebra (Interscience, New York, 1965).Google Scholar
2. Cohn, R. M., Systems of ideals, Can. J. Math. 21 (1969), 783–807.Google Scholar
3. Herzog, F., Systems of algebraic mixed difference equations, Trans. Amer. Math. Soc. 37 (1935), 286–300.Google Scholar
4. Kolchin, E. R., On the basis theorem for differential fields, Trans. Amer. Math. Soc. 52 (1942), 115–129.Google Scholar
5. Kolchin, E. R., Le théorème de la base finie pour les polynömes différentiels, Séminaire P. Dubreil, M.-L. Dubreil-Jacotin et C. Pisot, 14e Année: 1960/61, Algèbre et théorie des nombres, Fasc. 1 (Secrétariat mathématique, Paris, 1963).Google Scholar
6. Kolchin, E. R., Notes on differential algebra, unpublished.Google Scholar
7. Raudenbush, H. W., Ideal theory and algebraic differential equations, Trans. Amer. Math. Soc. 36 (1934), 361–368.Google Scholar
8. Raudenbush, H. W. and Ritt, J. F., Ideal theory and algebraic difference equations, Trans Amer. Math. Soc. 46 (1939), 445–452.Google Scholar
9. Ritt, J. F., Differential algebra, Amer. Math. Soc. Colloq. Publ., Vol. 33 (Amer. Math. Soc, Providence, R. I., 1950).Google Scholar
10. Seidenberg, A., Some basic theorems in differential algebra ﹛characteristic p, arbitrary), Trans. Amer. Math. Soc. 73 (1952), 174–190.Google Scholar
11. Strodt, W. C., Systems of algebraic partial difference equations, unpublished master's essay, Columbia University, New York, 1937.Google Scholar