No CrossRef data available.
Article contents
Dickson Polynomials of the Second Kind that are Permutations
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
It is known that the Dickson polynomial of the second kind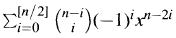 
permutes the elements of the finite prime field 
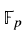(p odd) when n + 1 = ±2 to each of the moduli 
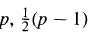and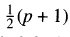 
. Based on numerical evidence it has been conjectured that these congruences are necessary for the polynomial to permute 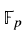. The conjecture is established here by a new method
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1994
References
1.
Brison, O. J., On group permutation polynomials, Portugal. Math.
50(1993), 365–383.Google Scholar
2.
Fried, M. and Lidl, R., On Dickson polynomials and Rédei functions, Proc. Salzburg Conf., Contributions to General Algebra 5, Springer-Verlag Holder-Pichler-Tempsky, Wien, 1987, 139–149.Google Scholar
3.
James, N. S. and Lidl, R., Permutation polynomials on matrices, Linear Algebra Appl.
96(1987), 181–190.Google Scholar
4.
Lidl, R. and Mullen, G. L., When does a polynomial over a finite field permute the elements of the field?, Amer. Math. Monthly
95(1988), 243–246.Google Scholar
5.
Lidl, R. and Niederreiter, H., Finite Fields, Encyclo. Math. Appls. 20, Addison-Wesley, Reading, Massachusetts, 1983.Google Scholar
6.
Matthews, R. W., Permutation polynomials in one and several variables, Ph.D. Dissertation, University of Tasmania, 1982.Google Scholar
7.
Mullen, G. L., Dickson polynomials over finite fields, Adv. in Math. (Beijing)
20(1991), 24–32.Google Scholar
You have
Access