Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:10:54.226Z Has data issue: false hasContentIssue false
  • English
  • Français

The Density of Redugible Integers

Published online by Cambridge University Press:  20 November 2018

S. D. Chowla  and
John Todd
S. D. Chowla
Affiliation:
Institute for Advanced Study, King's College, London
John Todd
Affiliation:
Institute for Advanced Study, King's College, London
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Introduction. The concept of a reducible integer was introduced recently [3] : if P(m) denotes the greatest prime factor of m then n is said to be reducible if P ( 1 + n2) < 2n. The reason for the term is that reducibility is a condition necessary and sufficient for the existence of a relation of the form 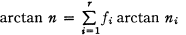where the ƒi are integers and the ni positive integers less than n. J. C. P. Miller pointed out to us the regularity of the distribution of the reducible integers (less than 600).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 1 , Issue 3 , 01 June 1949 , pp. 297 - 299
Copyright
Copyright © Canadian Mathematical Society 1949

References

[1] Chowla, S. and Vijayaraghavan, T., J . Indian Math. Soc. (New Series), vol. 11 (1947), 31–37.Google Scholar
[2] Landau, E., Handbuch der Lehre von der Verteilung der Primzahlen (Leipzig, 1909).Google Scholar
[3] Todd, John, “A Problem of J. C. P. Miller on Arctangent Relations,” Amer. Math. Monthly (1949).Google Scholar