Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:00:34.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Degree of Approximation by Rational Functions with Prescribed Numerator Degree

Published online by Cambridge University Press:  20 November 2018

D. Leviatan  and
D. S. Lubinsky
D. Leviatan
Affiliation:
Department of Mathematics Sackler Faculty of Science Tel Aviv University Ramat Aviv, Tel Aviv Israel
D. S. Lubinsky
Affiliation:
Department of Mathematics Witwatersrand University P.O. Wits 2050 South Africa
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a Jackson type theorem for rational functions with prescribed numerator degree: For continuous functions f: [—1,1] —> ℝ with ℓ sign changes in (—1,1), there exists a real rational function Rℓ,n(x) with numerator degree ℓ and denominator degree at most n, that changes sign exactly where f does, and such that

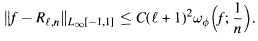
Here C is independent of f, n and ℓ, and ωφ is the Ditzian-Totik modulus of continuity. For special functions such as f(x) = sign(x)|x|α we consider improvements of the Jackson rate.

Keywords

41A2041A25rational approximationreal rational approximationJackson theoremsmoduli of continuityprescribed numerator degree
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 3 , 01 June 1994 , pp. 619 - 633
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. DeVore, R. A., Leviatan, D. and Yu, X. M., Lp Approximation by Reciprocals of Trigonometric and Algebraic Polynomials, Canad. Math. Bull. 33(1990), 460–469.Google Scholar
2. Ditzian, Z. and Totik, V., Moduli of Smoothness, Springer Series in Computational Math. 9, Springer-Verlag, New York, 1987.Google Scholar
3. Dombrowski, J. and Nevai, P., Orthogonal Polynomials, Measures and Recurrence Relations, SIAM J. Math. Anal. 17(1986), 752–759.Google Scholar
4. Leviatan, D., Levin, A. L. and Saff, E. B., On Approximation in the If-norm by Reciprocals of Polynomials, J. Approx. Theory 57(1989), 322–331.Google Scholar
5. Levin, A. L. and Lubinsky, D. S., Christoffel Functions, Orthogonal Polynomials, and Nevai's Conjecture for Freud Weights, Constr. Approx. 8(1992), 463–535.Google Scholar
6. Levin, A. L. and Saff, E. B., Degree of Approximation of Real Functions by Reciprocals of Real and Complex Polynomials, SIAM J. Math. Anal. 19(1988), 233–245.Google Scholar