Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T17:01:57.766Z Has data issue: false hasContentIssue false
  • English
  • Français

Degenerating sequences of conformal classes and the conformal Steklov spectrum

Part of: Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  05 March 2021

Vladimir Medvedev
Vladimir Medvedev*
Affiliation:
Département de Mathématiques et de Statistique, Pavillon André-Aisenstadt, Université de Montréal, Montréal, QC H3C 3J7, Canada and Peoples’ Friendship University of Russia (RUDN University), 6 Miklukho-Maklaya Street, Moscow 117198, Russian Federation and Faculty of Mathematics, National Research University Higher School of Economics, 6 Usacheva Street, Moscow 119048, Russian Federation
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 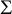$\Sigma $ be a compact surface with boundary. For a given conformal class c on 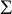$\Sigma $ the functional 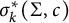$\sigma _k^*(\Sigma ,c)$ is defined as the supremum of the kth normalized Steklov eigenvalue over all metrics in c. We consider the behavior of this functional on the moduli space of conformal classes on 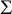$\Sigma $ . A precise formula for the limit of 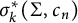$\sigma _k^*(\Sigma ,c_n)$ when the sequence 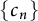$\{c_n\}$ degenerates is obtained. We apply this formula to the study of natural analogs of the Friedlander–Nadirashvili invariants of closed manifolds defined as 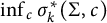$\inf _{c}\sigma _k^*(\Sigma ,c)$ , where the infimum is taken over all conformal classes c on 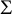$\Sigma $ . We show that these quantities are equal to 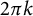$2\pi k$ for any surface with boundary. As an application of our techniques we obtain new estimates on the kth normalized Steklov eigenvalue of a nonorientable surface in terms of its genus and the number of boundary components.

Keywords

Spectral geometrySteklov spectrumupper boundsconformal Steklov spectrumcobordisms

MSC classification

Secondary: 35P15: Estimation of eigenvalues, upper and lower bounds
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 4 , August 2022 , pp. 1093 - 1136
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the Ministry of Science and Higher Education of the Russian Federation: agreement no. 075-03-2020-223/3 (FSSF-2020-0018).

References

Adams, D. and Hedberg, L., Function spaces and potential theory , Vol. 314. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar
Ahlfors, L., Open Riemann surfaces and extremal problems on compact subregions. Comment. Math. Helv. 24(1950), no. 1, 100–134.CrossRefGoogle Scholar
Banuelos, R., Kulczycki, T., Polterovich, I., and Siudeja, B., Eigenvalue inequalities for mixed Steklov problems. Oper. Theor. Appl. 231(2010), 19–34.Google Scholar
Bogosel, B., The Steklov spectrum on moving domains. Appl. Math. Optim. 75(2017), no. 1, 1–25.CrossRefGoogle Scholar
Borodzik, M., Némethi, A., and Ranicki, A., Morse theory for manifolds with boundary. Algebr. Geometr. Topol. 16(2016), no. 2, 971–1023.CrossRefGoogle Scholar
Buser, P., Geometry and spectra of compact Riemann surfaces. Vol. 106. Progress in Mathematics, Birkhäuser Boston, Inc., Boston, MA, 1992.Google Scholar
Colbois, B., El Soufi, A., and Girouard, A., Isoperimetric control of the Steklov spectrum. J. Funct. Anal. 261(2011), no. 5, 1384–1399.CrossRefGoogle Scholar
Colbois, B., El Soufi, A., and Girouard, A., Compact manifolds with fixed boundary and large Steklov eigenvalues. Proc. Am. Math. Soc. 147(2019), no. 9, 3813–3827.CrossRefGoogle Scholar
Colbois, B., Girouard, A., and Raveendran, B., The Steklov spectrum and coarse discretizations of manifolds with boundary. Pure Appl. Math. Quarter. 14(2018), no. 2, 357–392.CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G., and Valdinoci, E., Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136(2012), no. 5, 521–573.CrossRefGoogle Scholar
Enciso, A. and Peralta-Salas, D., Eigenfunctions with prescribed nodal sets. J. Differ. Geometry 101(2015), no. 2, 197–211.CrossRefGoogle Scholar
Fraser, A. and Schoen, R., The first Steklov eigenvalue, conformal geometry, and minimal surfaces. Adv. Math. 226(2011), no. 5, 4011–4030.CrossRefGoogle Scholar
Fraser, A. and Schoen, R., Minimal surfaces and eigenvalue problems. Geometr. Anal. Math. Relat. Nonlinear Partial Differ. Equat. 599(2012), 105–121.CrossRefGoogle Scholar
Fraser, A. and Schoen, R., Sharp eigenvalue bounds and minimal surfaces in the ball. Invent. Math. 203(2016), no. 3, 823–890.CrossRefGoogle Scholar
Fraser, A. and Schoen, R., Some results on higher eigenvalue optimization. Calculus Variat. Partial Differ. Equat. 59(2020), no. 5, 1–22.Google Scholar
Friedlander, L. and Nadirashvili, N., A differential invariant related to the first eigenvalue of the Laplacian. Int. Math. Res. Notices 17(1999), 939–952.CrossRefGoogle Scholar
Gabard, A., Sur la représentation conforme des surfaces de Riemann à bord et une caractérisation des courbes séparantes. Comment. Math. Helv. 81(2006), no. 4, 945–964.CrossRefGoogle Scholar
Girouard, A. and Lagacé, J., Large Steklov eigenvalues via homogenisation on manifolds. Preprint, 2020. arXiv:2004.04044 CrossRefGoogle Scholar
Girouard, A. and Polterovich, I., On the Hersch-Payne-Schiffer inequalities for Steklov eigenvalues. Funct. Anal. Appl. 44(2010), no. 2, 106–117.CrossRefGoogle Scholar
Girouard, A. and Polterovich, I., Spectral geometry of the Steklov problem (survey article). J. Spectr. Theory 7(2017), no. 2, 321–360.CrossRefGoogle Scholar
Girouard, A. and Polterovich, I., Upper bounds for Steklov eigenvalues on surfaces. Electronic Research Announcements, 19, 77.CrossRefGoogle Scholar
Hassannezhad, A., Conformal upper bounds for the eigenvalues of the Laplacian and Steklov problem. J. Funct. Anal. 261(2011), no. 12, 3419–3436.CrossRefGoogle Scholar
Henrot, A. and Pierre, M., Shape variation and optimization. Vol. 28. EMS Tracts in Mathematics. European Mathematical Society (EMS), Zürich, 2018. A geometrical analysis, English version of the French publication [MR2512810] with additions and updates.CrossRefGoogle Scholar
Hummel, C., Gromov’s compactness theorem for pseudo-holomorphic curves. Vol. 151. Progress in Mathematics, Birkhäuser Verlag, Basel, 1997.CrossRefGoogle Scholar
Jost, J., Bosonic Strings: A mathematical treatment. Vol. 21. American Mathematical Society, Providence, RI, 2007.CrossRefGoogle Scholar
Karpukhin, M., Upper bounds for the first eigenvalue of the Laplacian on non-orientable surfaces. IMRN 20(2016), 6200–6209.CrossRefGoogle Scholar
Karpukhin, M., Bounds between Laplace and Steklov eigenvalues on nonnegatively curved manifolds. Electron. Res. Announcements Math. Sci. 24(2017), 100–109.CrossRefGoogle Scholar
Karpukhin, M., Index of minimal spheres and isoperimetric eigenvalue inequalities. Invent. Math 223(2021), 335–377.CrossRefGoogle Scholar
Karpukhin, M., Kokarev, G., and Polterovich, I., Multiplicity bounds for Steklov eigenvalues on Riemannian surfaces. Ann. l’Institut Fourier 64(2014), no. 6, 2481–2502.CrossRefGoogle Scholar
Karpukhin, M. and Medvedev, V., On the Friedlander–Nadirashvili invariants of surfaces. Math. Ann. (2020), 1–39.Google Scholar
Karpukhin, M., Nadirashvili, N., Penskoi, A. V., and Polterovich, I., Conformally maximal metrics for Laplace eigenvalues on surfaces. Preprint, 2020. arXiv:2003.02871 CrossRefGoogle Scholar
Karpukhin, M. and Stern, D. L., Min-max harmonic maps and a new characterization of conformal eigenvalues. Preprint, 2020. arXiv:2004.04086 Google Scholar
Kokarev, G., Variational aspects of Laplace eigenvalues on Riemannian surfaces. Adv. Math. 258(2014), 191–239.CrossRefGoogle Scholar
Laurain, P. and Petrides, R., Regularity and quantification for harmonic maps with free boundary. Adv. Calculus Variat. 10(2017), no. 1, 69–82.CrossRefGoogle Scholar
Matthiesen, H. and Petrides, R., Free boundary minimal surfaces of any topological type in Euclidean balls via shape optimization. Preprint, 2020. arXiv:2004.06051 Google Scholar
Matthiesen, H. and Petrides, R., A remark on the rigidity of the first conformal Steklov eigenvalue. Preprint, 2020. arXiv:2006.04364 Google Scholar
Matthiesen, H. and Siffert, A., Sharp asymptotics of the first eigenvalue on some degenerating surfaces. Trans. Am. Math. Soc. 373(2020), no. 8, 5903–5936.CrossRefGoogle Scholar
Nadirashvili, N. and Sire, Y., Conformal spectrum and harmonic maps. Moscow Math. J. 15(2015), no. 1, 123–140.CrossRefGoogle Scholar
Nadirashvili, N. and Sire, Y., Maximization of higher order eigenvalues and applications. Moscow Math. J. 15(2015), no. 4, 767–775.CrossRefGoogle Scholar
Osgood, B., Phillips, R., and Sarnak, P., Extremals of determinants of Laplacians. J. Funct. Anal. 80(1988), no. 1, 148–211.CrossRefGoogle Scholar
Penskoĭ, A. V., Extremal metrics for the eigenvalues of the Laplace-Beltrami operator on surfaces (Russian). Uspekhi Mat. Nauk 68(2013), no. 414, 107–168.Google Scholar
Penskoĭ, A. V., Isoperimetric inequalities for higher eigenvalues of the Laplace-Beltrami operator on surfaces (Russian). Trudy Matematicheskogo Instituta Imeni V. A. Steklova, 305, Algebraicheskaya Topologiya Kombinatorika i Matematicheskaya Fizika, 2019, pp. 291–308.CrossRefGoogle Scholar
Petrides, R., Existence and regularity of maximal metrics for the first Laplace eigenvalue on surfaces. Geometr. Funct. Anal. 24(2014), no. 4, 1336–1376.CrossRefGoogle Scholar
Petrides, R., On the existence of metrics which maximize Laplace eigenvalues on surfaces. IMRN 2018(2018), no. 14, 4261–4355.CrossRefGoogle Scholar
Petrides, R., Maximizing Steklov eigenvalues on surfaces. J. Differ. Geometry 113(2019), no. 1, 95–188.CrossRefGoogle Scholar
Rauch, J. and Taylor, M., Potential and scattering theory on wildly perturbed domains. J. Funct. Anal. 18(1975), no. 1, 27–59.CrossRefGoogle Scholar
Schoen, R., Existence and geometric structure of metrics on surfaces which extremize eigenvalues. Bull. Braz. Math. Soc. (N.S.) 44(2013), no. 4, 777–807.CrossRefGoogle Scholar
Taylor, M. E., Partial differential equations I. Basic theory. 2nd ed. Applied Mathematical Sciences, 117, Springer, 2011.CrossRefGoogle Scholar
Weinstock, R., Inequalities for a classical eigenvalue problem. J. Rational Mech. Anal. 3(1954), 745–753.Google Scholar
Wolf, S. A. and Keller, J. B., Range of the first two eigenvalues of the Laplacian. Proc. R. Soc. Lond. A. 447(1994), no. 1930, 397–412.Google Scholar
Yang, P. C. and Yau, S. T., Eigenvalues of the Laplacian of compact Riemann surfaces and minimal submanifolds. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 7(1980), no. 1, 55–63.Google Scholar