Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T18:19:11.734Z Has data issue: false hasContentIssue false
  • English
  • Français

Cuntz Algebra States Defined by Implementers of Endomorphisms of the CAR Algebra

Published online by Cambridge University Press:  20 November 2018

Michael J. Gabriel
Michael J. Gabriel*
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, 585 King Edward Avenue, Ottawa, Ontario, K1N 6N5, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate representations of the Cuntz algebra ${{\mathcal{O}}_{2}}$ on antisymmetric Fock space ${{F}_{a}}({{\mathcal{K}}_{1}})$ defined by isometric implementers of certain quasi-free endomorphisms of the CAR algebra in pure quasi-free states $\varphi {{P}_{1}}$. We pay special attention to the vector states on ${{\mathcal{O}}_{2}}$ corresponding to these representations and the Fock vacuum, for which we obtain explicit formulae. Restricting these states to the gauge-invariant subalgebra 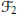${{\mathcal{F}}_{2}}$, we find that for natural choices of implementers, they are again pure quasi-free and are, in fact, essentially the states $\varphi {{P}_{1}}$. We proceed to consider the case for an arbitrary pair of implementers, and deduce that these Cuntz algebra representations are irreducible, as are their restrictions to 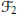${{\mathcal{F}}_{2}}$.

The endomorphisms of $B\left( {{F}_{a}}({{\mathcal{K}}_{1}}) \right)$ associated with these representations of ${{\mathcal{O}}_{2}}$ are also considered.

Keywords

46L0546L30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 4 , 01 August 2002 , pp. 694 - 708
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Araki, H., On quasifree states of CAR and Bogoliubov automorphisms. Publ. Res. Inst. Math. Sci. 6(1970/71), 385–442.Google Scholar
[2] Binnenhei, C., Implementation of endomorphisms of the CAR algebra. Rev. Math. Phys. 7 (1995), 833–869.Google Scholar
[3] Bratteli, O., Jorgensen, P. E. T. and Price, G. L., Endomorphisms of B(H). In: Quantization of Nonlinear Partial Differential Equations (eds. W. B. Arveson et al.), Proc. Sympos. Pure Math. 59 (1996), 93–138.Google Scholar
[4] Bratteli, O. and Jorgensen, P. E. T., A connection between multiresolution theory of scale N and representations of the Cuntz algebra ON. In: Operator Algebras and Quantum Field Theory (Rome 1996), Internat. Press, Cambridge, MA, 1997, 151–163.Google Scholar
[5] Bratteli, O. and Jorgensen, P. E. T., Endomorphisms of B(H) II. Finitely Correlated States on On . J. Funct. Anal. (2) 145 (1997), 323–373.Google Scholar
[6] Bratteli, O. and Jorgensen, P. E. T., Isometries, Shifts, Cuntz algebras and multiresolution wavelet analysis of scale N. Integral Equations Operator Theory (4) 28 (1997), 382–443.Google Scholar
[7] Cuntz, J., Simple C*-algebras generated by isometries. Comm. Math. Phys. 57 (1977), 173–185.Google Scholar
[8] Doplicher, S. and Roberts, J. E., Fields, statistics and non-abelian gauge groups. Comm. Math. Phys. 28 (1972), 331–348.Google Scholar
[9] Doplicher, S. and Roberts, J. E., Why there is a field algebra with a compact gauge group describing the superselection structure in particle physics. Comm. Math. Phys. (1) 131 (1990), 51–107.Google Scholar
[10] Evans, D. E. and Kawahigashi, Y., Quantum Symmetries on Operator Algebras. Oxford University Press, 1998.Google Scholar
[11] Gabriel, M. J., Quasi-free Maps of the CAR, Cuntz and Pimsner Algebras. PhD Thesis, University of Wales, Swansea, July 2000.Google Scholar
[12] Jeong, E., Irreducible representations of the Cuntz algebra On . Proc. Amer. Math. Soc. (12) 127 (1999), 3583–3590.Google Scholar
[13] Laca, M., Endomorphisms of B(H) and Cuntz algebras. J. Operator Theory (1) 30 (1993), 85–108.Google Scholar
[14] Roberts, J. E., Cross products of von Neumann algebras by group duals. Symposia Mathematica Vol. XX, Academic Press, London, 1976, 335–363.Google Scholar
[15] Ruijsenaars, S. N. M., On Bogoliubov Transformations. II. The General Case. Ann. Physics 116 (1978), 105–134.Google Scholar