Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T00:39:15.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Cubic Polynomials with Periodic Cycles of a Specified Multiplier

Published online by Cambridge University Press:  20 November 2018

Patrick Ingram
Patrick Ingram*
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON and Department of Mathematics, Colorado State University, Fort Collins, CO, USA email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider cubic polynomials 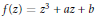$f\left( z \right)\,=\,{{z}^{3}}\,+\,az\,+\,b$ defined over 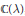$\mathbb{C}\left( \lambda \right)$, with a marked point of period 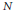$N$ and multiplier 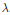$\lambda$. In the case 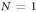$N\,=\,1$, there are infinitely many such objects, and in the case 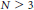$N\,\ge \,3$, only finitely many (subject to a mild assumption). The case 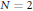$N\,=\,2$ has particularly rich structure, and we are able to describe all such cubic polynomials defined over the field 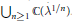${{\cup }_{n\ge 1}}\,\mathbb{C}\left( {{\lambda }^{1/n}} \right)$.

Keywords

37P35cubic polynomialsperiodic pointsholomorphic dynamics
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 2 , 16 April 2012 , pp. 318 - 344
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Berker, S., Epstein, A. L., and Pilgrim, K. M., Remarks on the period three cycles of quadratic rational maps. Nonlinearity 16(2003), no. 1, 93–100. http://dx.doi.org/10.1088/0951-7715/16/1/306 Google Scholar
[2] Bonifant, A., Kiwi, J. and Milnor, J. Cubic polynomial maps with periodic critical point. II. Escape regions. Conform. Geom. Dyn. 14(2010), 68–112. http://dx.doi.org/10.1090/S1088-4173-10-00204-3 Google Scholar
[3] Fastenberg, L. A., Computing the Mordell-Weil ranks of cyclic covers of elliptic surfaces. Proc. Amer. Math. Soc. 129(2001), no. 7, 1877–1883. http://dx.doi.org/10.1090/S0002-9939-01-06152-4 Google Scholar
[4] Hindry, M. and Silverman, J. H., The canonical height and integral points on elliptic curves. Invent. Math. 93(1988), no. 2, 419–450. http://dx.doi.org/10.1007/BF01394340 Google Scholar
[5] Milnor, J., Remarks on iterated cubic maps. Experiment. Math. 1(1992), no. 1, 5–24.Google Scholar
[6] Milnor, J., Dynamics in one complex variable. Third ed. Annals of Mathematics Studies, 160, Princeton University Press, Princeton, NJ, 2006.Google Scholar
[7] Morton, P., On certain algebraic curves related to polynomial maps. Compositio Math. 103(1996), no. 3, 319–350.Google Scholar
[8] Shaferevich, I. R., Basic Algebraic Geometry 1. Varieties in projective space. Second ed. Spring-Verlag, Berlin, 1994.Google Scholar
[9] Shioda, T., On the Mordell-Weil lattices. Comment. Math. Univ. St. Paul. 39(1990), no. 2, 211–240.Google Scholar
[10] Silverman, J. H., The Arithmetic of dynamical systems. Graduate texts in mathematics, 241, Springer, New York, 2007.Google Scholar
[11] Vojta, P., Mordell's conjecture over function fields. Invent. Math. 98(1989), 115–138. http://dx.doi.org/10.1007/BF01388847Google Scholar