Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:00:53.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Criteria for Biquadratic Residuacity Modulo a Prime p involving Quaternary Representations of p

Published online by Cambridge University Press:  20 November 2018

Kenneth S. Williams ,
Christian Friesen  and
Lawrence J. Howe
Kenneth S. Williams
Affiliation:
Carleton University, Ottawa, Ontario
Christian Friesen
Affiliation:
Carleton University, Ottawa, Ontario
Lawrence J. Howe
Affiliation:
Carleton University, Ottawa, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1958, Hasse [10, p. 236], in connection with his work on the 2n-th power character of 2 in the cyclotomic field Q(exp(2πi/2n)), proved that for every prime p ≡ 1 (mod 16) the pair of equations

is always solvable in integers x, u, v, w. Later in 1972 Giudici, Muskat, and Robinson [7, p. 388] showed in their work on Brewer's character sums that Hasse's system is also solvable for primes p ≡ 7 (mod 16). Moreover they also showed [7, p. 345] that for primes p ≡ 1 (mod 5) the pair of equations

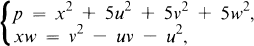
is solvable in integers x, u, v, w. In this paper we consider a pair of diophantine equations (involving a prime p and an integer m) which includes, the above two systems as the special cases when m = 2 and m = 5. The system is then used to give criteria for m to be a biquadratic residue modulo p.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 2 , 01 April 1985 , pp. 337 - 370
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Berndt, B. C. and Evans, R. J., Sums of Gauss, Jacobi and Jacobsthal J. Number Theory 11 (1979), 349–398.Google Scholar
2. Berndt, B. C. and Evans, R. J., Sums of Gauss, Eisenstein, Jacobi, Jacobsthal, and Brewer, Illinois J. Math. 23 (1979), 374–437.Google Scholar
3. Brown, E. and Parry, C. J., The 2-class group of certain biquadratic number fields, J. reine und angewandte Math. 295 (1977), 61–71.Google Scholar
4. Brown, E. and Parry, C. J., The 2-class group of biquadratic fields, II, Pacific J. Math. 78 (1978), 11–26.Google Scholar
5. Dickson, L. E., Cyclotomy, higher congruences, and Waring's problem. Amer. J. Math. 57 (1935), 391–424.Google Scholar
6. Edgar, H. and Peterson, B., Some contributions to the theory of cyclic quartic extensions oj the rationals, J. Number Theory 12 (1980), 77–83.Google Scholar
7. Giudici, R. E., Muskat, J. B. and Robinson, S. F., On the evaluation of Brewer's character sums, Trans. Amer. Math. Soc. 171 (1972), 317–347.Google Scholar
8. Gras, M.-N., Z-bases d'entiers 1, Θ, Θ2, Θ3 dans les extensions cycliques de degré 4 de Q, Publications Mathématiques de la Faculté des Sciences de Besançon, Années 1979–1980 et 1980–1981, Théorie des Nombres, 14 pp.Google Scholar
9. Hasse, H., Arithmetische Bestimmung von Grundeinheit und Klassenzahl in zyklischen kubischen und biquadratischen Zahlkôrpem, Abh. Deutsch. Akad. Wiss. Berlin, Math. 2 (1948). 1–95.Google Scholar
10. Hasse, H., Der 2n-te Potenzcharakter von 2 im Körper der 2n-ten Einheitswurzeln, Rend. Cire. Mat. Palermo 7 (1958), 185–244.Google Scholar
11. Hudson, R. H. and Williams, K. S., Some new residuacity criteria, Pacific J. Math. 91 (1980), 135–143.Google Scholar
12. Hudson, R. H. and Williams, K. S., Extension of a theorem of Cauchy and Jacobi, to appear in Journal of Number Theory.Google Scholar
13. Lehmer, E., Criteria for cubic and quartic residuacity, Mathematika 5 (1958), 20–29.Google Scholar
14. Long, R. L., Algebraic number theory (Marcel Dekker, Inc., New York, 1977).Google Scholar
15. Muskat, J. B. and Zee, Y.-C., On the uniqueness of certain diophantine equations, Proc. Amer. Math. Soc. 49 (1975), 13–19.Google Scholar
16. Zee, Y.-C., The Jacobi sums of orders thirteen and sixty and related quadratic decompositions, Math. Z. 115 (1970), 259–272.Google Scholar