Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T08:55:23.303Z Has data issue: false hasContentIssue false
  • English
  • Français

Criteres de G-Stabilite en Termes de Transversalite

Published online by Cambridge University Press:  20 November 2018

Jean-Jacques Gervais
Jean-Jacques Gervais*
Affiliation:
Université Laval, Québec, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1.1. Introduction. Soit G un sous-groupe de Lie, de dimension q, du groupe GLP(R). Soient Gi(n) = Ci0,e(Rn, G) le groupe des germes en 0 des applications g de classe Ci de Rn dans G telles que g(0) = e (où e est l'élément neutre de G); Diffi(n) le groupe des germes en 0 des difféomorphismes τ d'un voisinage de 0 dans Rn sur un voisinage de 0 dans Rn tels que τ(0) = 0; C0i(Rn, Rp) l'ensemble des germes en 0 des applications de classe Ci de Rn dans Rp; 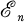l'anneau des germes en 0 des fonctions numériques de classe C∞ sur Rn et m son idéal maximal. Pour ƒ ∈ C0∞(Rn, Rp), nous désignerons par jr(ƒ) le jet d'ordre r de ƒ en 0. On munit l'ensemble de la structure de groupe définie par la multiplication:

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 2 , 01 April 1979 , pp. 264 - 273
Copyright
Copyright © Canadian Mathematical Society 1979

References

Bibliographie

1. Merrien, J., Idéaux de l'anneau des séries formelles à coefficients réels et variétés associées, J. Math. pures et appl, 50, (1971), 169–187.Google Scholar
2. Tougeron, J.-Cl., ℊ-stabilité des germes d'applications différentiables, Séminaire d'Analyse de Rennes (1971).Google Scholar
3. Tougeron, J.-Cl., Idéaux de fonctions différentiables, Ergebnisse Band 71, Springer-Verlag (1972).Google Scholar
4. Tougeron, J.-Cl., Solutions d'un système d﹜équations analytiques réelles et applications, Ann. Inst. Fourier, 26, Fasc. 3, (1976), 109–135.Google Scholar