Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T15:10:40.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Coxeter Diagrams and the Köthe’s Problem

Part of: Modules, bimodules and ideals Representation theory of rings and algebras

Published online by Cambridge University Press:  24 February 2020

Ziba Fazelpour  and
Alireza Nasr-Isfahani
Ziba Fazelpour
Affiliation:
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395-5746, Tehran, Iran e-mail: [email protected]
Alireza Nasr-Isfahani
Affiliation:
Department of Pure Mathematics, Faculty of Mathematics and Statistics, University of Isfahan, P.O. Box: 81746-73441, Isfahan, Iran and School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395-5746, Tehran, Iran e-mail: [email protected]@ipm.ir
Get access Rights & Permissions [Opens in a new window]

Abstract

A ring 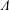$\unicode[STIX]{x1D6EC}$ is called right Köthe if every right 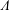$\unicode[STIX]{x1D6EC}$-module is a direct sum of cyclic modules. In this paper, we give a characterization of basic hereditary right Köthe rings in terms of their Coxeter valued quivers. We also give a characterization of basic right Köthe rings with radical square zero. Therefore, we give a solution to Köthe’s problem in these two cases.

Keywords

right Köthe ringrepresentation-finite ringspeciespartial Coxeter functorCoxeter functorCoxeter valued quiverseparated diagram

MSC classification

Primary: 16G10: Representations of Artinian rings
Secondary: 16D70: Structure and classification (except as in ), direct sum decomposition, cancellation 16G60: Representation type (finite, tame, wild, etc.)
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 3 , June 2021 , pp. 656 - 686
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the first author was in part supported by a grant from IPM. Also, the research of the second author was in part supported by a grant from IPM (No. 98170412).

References

Anderson, F. W. and Fuller, K. R., Rings and categories of modules, Second ed., Graduate Texts in Mathematics, 13, Springer-Verlag, New York, 1992. https://doi.org/10.1007/978-1-4612-4418-9CrossRefGoogle Scholar
Assem, I., Simson, D., and Skowronski, A., Elements of the representation theory of associative algebras. Vol. 1, Techniques of representation theory, London Mathematical Society Student Texts, 65, Cambridge University Press, Cambridge, 2006. https://doi.org/10.1017/CBO9780511614309CrossRefGoogle Scholar
Auslander, M., Large modules over Artin algebras. In: Algebra, topology and category theory. Academic Press, New York, 1976, pp. 1–17.Google Scholar
Auslander, M., Platzeck, M. I., and Reiten, I., Coxeter functors without diagrams. Trans. Amer. Math. Soc. 250(1979), 1–46. https://doi.org/10.2307/1998978CrossRefGoogle Scholar
Auslander, M., Reiten, I., and Smalo, S. O., Representation theory of Artin algebras. Cambridge Studies in Advanced Mathematics, 36, Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Behboodi, M., Ghorbani, A., Morazadeh-Dehkordi, A., and Shojaee, S. H., On left Köthe rings and a generalization of a Köthe–Cohen–Kaplansky theorem. Proc. Amer. Math. Soc. 142(2014), no. 8, 2625–2631. https://doi.org/10.1090/S0002-9939-2014-11158-0CrossRefGoogle Scholar
Bernstein, I. N., Gelfand, I. M., and Ponomarev, V. A., Coxeter functors, and Gabriel’s theorem . (Russian) Uspehi Mat. Nauk 28(1973), no. 2(170), 19–33.Google Scholar
Bourbaki, N., Lie groups and Lie algebras. Chapters 4–6. Translated from the 1968 French orginal by Andrew Pressley. Elements of Mathematics (Berlin), Springer-Verlag, Berlin, 2002. https://doi.org/doi.org/10.1007/978-3-540-89394-3CrossRefGoogle Scholar
Chase, S. U., Direct products of modules . Trans. Amer. Math. Soc. 97(1960), 457–473. https://doi.org/10.2307/1993382CrossRefGoogle Scholar
Cohen, I. S. and Kaplansky, I., Rings for which every module is a direct sum of cyclic modules . Math. Z. 54(1951), 97–101. https://doi.org/10.1007/BF01179851CrossRefGoogle Scholar
Dlab, V. and Ringel, C. M., Indecomposable representations of graphs and algebras . Mem. Amer. Math. Soc. 6(1976), no. 173. https://doi.org/10.1090/memo/0173Google Scholar
Dlab, V. and Ringel, C. M., On algebras of finite representation type . J. Algebra 33(1975), 306–394. https://doi.org/10.1016/0021-8693(75)90125-8CrossRefGoogle Scholar
Dowbor, P., Ringel, C. M., and Simson, D., Hereditary Artinian rings of finite representation type . In: Representation theory, II (Proc. Second Internat. Conf., Carleton Univ., Ottawa, Ont., 1979) . Lecture Notes in Math., 832, Springer, Berlin, 1980, pp. 232–241.Google Scholar
Dowbor, P. and Simson, D., A characterization of hereditary rings of finite representation type . Bull. Amer. Math. Soc. (N.S.) 2(1980), no. 2, 300–302. https://doi.org/10.1090/S0273-0979-1980-14741-2 CrossRefGoogle Scholar
Dowbor, P. and Simson, D., Quasi-Artin species and rings of finite representation type . J. Algebra 63(1980), no. 2, 435–443. https://doi.org/10.1016/0021-8693(80)90082-4 CrossRefGoogle Scholar
Drozd, J. A., The structure of hereditary rings . (Russian) Mat. Sb. (N.S.) 113(155)(1980), no. 1(9), 161–172, 176.Google Scholar
Fazelpour, Z. and Nasr-Isfahani, A., Connection between representation-finite and Köthe rings. J. Algebra 514(2018), 25–39. https://doi.org/10.1016/j.jalgebra.2018.08.006CrossRefGoogle Scholar
Fossum, R. M., Griffith, P. A., and Reiten, I., Trivial extensions of Abelian categories. Homological algebra of trivial extensions of abelian categories with applications to ring theory. Lecture Notes in Mathematics, 456, Springer-Verlag, Berlin–New York, 1975.Google Scholar
Gabriel, P., Indecomposable representation. II. Symposia Mathematica, Vol. XI (Convegno di Algebra Commutativa, INDAM, Rome, 1971), Academic Press, London, 1973, pp. 81–104.Google Scholar
Gabriel, P., Unzerlegbare Darstellungen I . Manuscripta Math. 6(1972), 71–103; correction, ibid. 6(1972), 309. https://doi.org/10.1007/BF01298413 CrossRefGoogle Scholar
Goodearl, K. R. and Warfield, R. B. Jr., An introduction to noncommutative Noetherian rings , Second ed., London Mathematical Society Student Texts, 61, Cambridge University Press, Cambridge, 2004. https://doi.org/10.1017/CBO9780511841699 CrossRefGoogle Scholar
Griffith, P., On the decomposition of modules and generalized left uniserial rings . Math. Ann. 184(1969/1970), 300–308. https://doi.org/10.1007/BF01350858 CrossRefGoogle Scholar
Haghany, A. and Varadarajan, K., Study of modules over formal triangular matrix rings. J. Pure Appl. Algebra 147(2000), no. 1, 41–58. https://doi.org/10.1016/S0022-4049(98)00129-7CrossRefGoogle Scholar
Humphreys, J. E., Reflection groups and Coxeter groups . Cambridge studies in Advanced Mathematics, 29, Cambridge University Press, Cambridge, 1990. https://doi.org/10.1017/CBO9780511623646 CrossRefGoogle Scholar
Kawada, Y., On Köthe’s problem concerning algebras for which every indecomposable module is cyclic I. Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 7(1962), 154–230.Google Scholar
Kawada, Y., On Köthe’s problem concerning algebras for which every indecomposable module is cyclic II. Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 8(1963), 1–62.Google Scholar
Kawada, Y., On Köthe’s problem concerning algebras for which every indecomposable module is cyclic III. Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 8(1965), 165–250.Google Scholar
Köthe, G., Verallgemeinerte Abelsche Gruppen mit hyperkomplexem Operatorenring. (German) Math. Z. 39(1935), no. 1, 31–44. https://doi.org/10.1007/BF01201343CrossRefGoogle Scholar
Nakayama, T., Note on uni-serial and generalized uni-serial rings . Proc. Imp. Acad. Tokyo 16(1940), 285–289.Google Scholar
Prüfer, H., Untersuchungen über die Zerlegbarkeit der Abzählbaren primären abelschen Gruppen . (German) Math. Z. 17(1923), no. 1, 35–61. https://doi.org/10.1007/BF01504333 CrossRefGoogle Scholar
Ringel, C. M., Kawada’s theorem . In: Abelian group theory (Oberwolfach, 1981) . Lecture Notes in Math., 874, Springer, Berlin–New York, 1981, pp. 431–447.CrossRefGoogle Scholar
Ringel, C. M., Representation theory of Dynkin quivers, Three contributions. Front. Math. China 11(2016), no. 4, 765–814. https://doi.org/10.1007/s11464-016-0548-5 CrossRefGoogle Scholar
Ringel, C. M., Representations of K-species and bimodules . J. Algebra 41(1976), no. 2, 269–302. https://doi.org/10.1016/0021-8693(76)90184-8 CrossRefGoogle Scholar
Schofield, A. H., Hereditary artinian rings of finite representation type and extensions of simple artinian rings. Math. Proc. Cambridge Philos. Soc. 102(1987), no. 3, 411–420. https://doi.org/10.1017/S0305004100067463 CrossRefGoogle Scholar
Schofield, A. H., Representations of rings over skew fields. London Mathematical Society Lecture Note Series, 92, Cambridge University Press, Cambridge, 1985. https://doi.org/10.1017/CBO9780511661914 CrossRefGoogle Scholar
Simson, D., A class of potential counterexamples to the pure semisimplicity conjecture. In: Advances in algebra and model theory (Essen, 1994; Dresden, 1995). Algebra Logic Appl., 9, Gordon and Breach, Amsterdam, 1997, pp. 345–373.Google Scholar
Simson, D., An Artin problem for division ring extensions and the pure semisimplicity conjecture II. J. Algebra 227(2000), no. 2, 670–705. https://doi.org/10.1006/jabr.1999.8245 CrossRefGoogle Scholar
Simson, D., Categories of representations of species . J. Pure Appl. Algebra 14(1979), no. 1, 101–114. https://doi.org/10.1016/0022-4049(79)90015-X CrossRefGoogle Scholar
Simson, D., On right pure semisimple hereditary rings and an Artin problem . J. Pure Appl. Algebra 104(1995), no. 3, 313–332. https://doi.org/10.1016/0022-4049(94)00068-X CrossRefGoogle Scholar
Simson, D., Partial Coxeter functors and right pure semisimple hereditary rings . J. Algebra 71(1981), no. 1, 195–218. https://doi.org/10.1016/0021-8693(81)90115-0 CrossRefGoogle Scholar
Simson, D., Pure semisimple categories and rings of finite representation type . J. Algebra 48(1977), no. 2, 290–296. https://doi.org/10.1016/0021-8693(77)90307-6 CrossRefGoogle Scholar
Simson, D., Pure semisimple categories and rings of finite representation type, Corrigendum . J. Algebra 67(1980), no. 1, 254–256. https://doi.org/10.1016/0021-8693(80)90320-8 CrossRefGoogle Scholar
Wisbauer, R., Foundations of module and ring theory. A handbook for study and research. Revised and translated from the 1988 German edition, Algebra, Logic and Applications, 3, Gordon and Breach Science Publishers, Philadelphia, PA, 1991.Google Scholar