Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:38:52.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Covering Theorems for Classes of Univalent Functions

Published online by Cambridge University Press:  20 November 2018

Dov Aharonov  and
W. E. Kirwan
Dov Aharonov
Affiliation:
University of Maryland, College Park, Maryland
W. E. Kirwan
Affiliation:
University of Maryland, College Park, Maryland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let denote the class of functions f(z) = z + that are analytic and univalent in 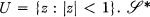and will denote the collection of f ∈ that map U onto a domain that is respectively starlike with respect to the origin and convex.

In [4, p. 85] Hayman used Steiner symmetrization to solve a problem, a special case of which is the following.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 25 , Issue 2 , April 1973 , pp. 412 - 419
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Aharonov, D. and Kirwan, W. E., A method of symmetrization and applications, Trans Amer. Math. Soc. (to appear).Google Scholar
2. Aharonov, D. and Kirwan, W. E., A method of symmetrization and applications, II (to appear).Google Scholar
3. Frantz, W. and Kratzer, A., Tranzendente Functionen (Akademische Verlagsgesellschaft, Leipzig, 1960).Google Scholar
4. Hayman, W. K., Multivalent functions (Cambridge University Press, Cambridge, 1958).Google Scholar
5. Jenkins, J. A., On values omitted by univalent functions, Amer. J. Math. 2 (1953), 406–408.Google Scholar
6. Klein, M., Estimates for the transfinite diameter with applications to conformai mapping, Pacific J. Math. 22 (1967), 267–279.Google Scholar
7. Lewandowski, Z., On circular symmetrization of starlike functions, Ann. Univ. Mariae Curie-Sklodowska Sect. A 17 (1963), 35–37.Google Scholar
8. Löwner, K., Untersuchengen über die Verzerrung bei konformen Abbildungen des Einheitskreises, die durch Functionen mit nicht Verschwindender Ableitung geliefert werden, Berichte Könige. Sachs. Ges. Wissen, Leipzig 69 (1917), 89–106.Google Scholar
9. Nehari, Z., Conformai mapping (McGraw-Hill, New York, 1952).Google Scholar
10. Strohhäcker, E., Beiträgezur Théorie der Schlichten Functionen, Math. Z. 37 (1933), 356–380.Google Scholar