Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T16:52:31.154Z Has data issue: false hasContentIssue false
  • English
  • Français

A Counterexample in Lp Approximation by Harmonic Functions

Published online by Cambridge University Press:  20 November 2018

Joan Mateu
Joan Mateu*
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra (Barcelona), Spain e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 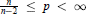we show that the conditions 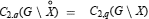for all open sets G, C2,q denoting Bessel capacity, are not sufficient to characterize the compact sets X with the property that each function harmonic on 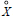and in Lp(X) is the limit in the Lp norm of a sequence of functions which are harmonic on neighbourhoods of X.

Keywords

41A3031C15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 49 , Issue 3 , 01 June 1997 , pp. 568 - 582
Copyright
Copyright © Canadian Mathematical Society 1997

References

[AH] Adams, D.R., Hedberg, L.I., Function spaces and potential theory, Springer, Berlin and Heidelberg, 1996.Google Scholar
[Ba] Bagby, T., Approximation in the mean by solutions of elliptic equations, Trans. Amer. Math. Soc. 281(1984), 761–784.Google Scholar
[Br] Brelot, M., Sur les ensembles effilés, Bull. Sci. Math. 68(1944), 12–36.Google Scholar
[C] Carleson, L., Selected problems on exceptional sets, Van Nostrand, Princeton, New Jersey, 1967.Google Scholar
[G] Gamelin, T.W., Uniform Algebras, Prentice Hall, Englewood Cliff, New Jersey, 1969.Google Scholar
[H1] Hedberg, L.I., Non-linear potentials and approximation in the mean by analytic functions, Math. Z. 129(1972), 299–319.Google Scholar
[H2] Hedberg, L.I., Approximation in the mean by solutions of elliptic equations, Duke Math. J. 40(1973), 9–16.Google Scholar
[H3] Hedberg, L.I., Two approximation problems in function spaces, Ark.Mat. 16(1978), 51–81.Google Scholar
[H4] Hedberg, L.I., Spectral synthesis in Sobolev spaces, and uniqueness of solutions of the Dirichlet problem, Acta Math. 147(1981), 237–264.Google Scholar
[HW] Hedberg, L.I. and Wolff, T., Thin sets in nonlinear potential theory, Ann. Inst. Fourier (Grenoble) (4) 33(1983), 161–187.Google Scholar
[MNOV] Mateu, J., Netrusov, Y., Orobitg, J. and Verdera, J., BMO and Lipschitz approximation by solutions of elliptic equations, Ann. Inst. Fourier (Grenoble) (4) 46(1996), 1057–1081.Google Scholar
[Me] Meyers, N.G., A theory of capacities for potentials of functions in Lebesgue classes, Math. Scand. 26(1970), 225–292.Google Scholar
[O] O’Farrell, A.G., Hausdorff content and rational approximation in fractional Lipschitz norms, Trans.Amer. Math. Soc. 228(1977), 187–206.Google Scholar
[P] Polking, J.C., Approximation in Lp by solutions of elliptic partial differential equations, Amer. J. Math. 94(1972), 1231–1244.Google Scholar
[S] Stein, E.M., Singular integrals and differentiability properties of functions, Princeton University Press, Princeton, New Jersey, 1970.Google Scholar