Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T12:30:13.148Z Has data issue: false hasContentIssue false
  • English
  • Français

Convolution Transforms Related To Non-Harmonic Fourier Series

Published online by Cambridge University Press:  20 November 2018

D. B. Sumner
D. B. Sumner*
Affiliation:
Hamilton College, McMaster University, and Research Institute of the Canadian Mathematical Congress
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. Widder has pointed out (2, p. 219) in connection with Wiener's fundamental work on the operational calculus (1, pp. 557-584), that the convolution transform

(1.1)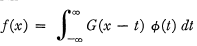

will be inverted by the operator DE (D), where D = d/dx, and

,

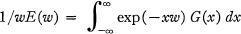where a suitable interpretation must be found for E(D).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 7 , 1955 , pp. 89 - 100
Copyright
Copyright © Canadian Mathematical Society 1955

References

1. Wiener, N., The operational calculus, Math. Ann., 95 (1925-26), 557–584.Google Scholar
2. Widder, D. V., Inversion formulas for convolution transforms, Duke Math. J., 14 (1947), –.Google Scholar
3. Widder, D. V., The Stieltjes transform, Trans. Amer. Math. Soc, 43 (1938), 7–60.Google Scholar
4. Hirschmann, I. I., Jr. and Widder, D. V., Generalized inversion formulas for convolution transforms, Duke Math. J., 15 (1948), 659–696.Google Scholar
5. Sumner, D. B., An inversion formula for the generalized Stieltjes transform, Bull. Amer. Math. Soc, 55 (1949), 174–183.Google Scholar
6. Hirschmann, I. I., Jr. and Widder, D. V., Convolution transforms with complex kernels, Pacific J. Math., 1 (1951), 211–225.Google Scholar
7. Levinson, N., Gap and density theorems (Amer. Math. Soc. Coll., vol. XXVI, 1940).Google Scholar
8. Hirschmann, I. I., Jr. and Widder, D. V., Inversion of a class of convolution transforms, Trans. Amer. Math. Soc, 66 (1949), 135–201.Google Scholar
9. Titchmarsh, E. C., The theory of functions (1st. ed., Oxford, 1932).Google Scholar
10. Hardy, G. H. and Levinson, N., Inequalities satisfied by a certain definite integral. Bull. Amer. Math. Soc, 43 (1937), 709–716.Google Scholar