Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T02:33:53.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Convolution of Trace Class Operators over Locally Compact Quantum Groups

Published online by Cambridge University Press:  20 November 2018

Zhiguo Hu ,
Matthias Neufang  and
Zhong-Jin Ruan
Zhiguo Hu
Affiliation:
Department of Mathematics and Statistics, University of Windsor, Windsor, Ontario, N9B 3P4, e-mail: [email protected]
Matthias Neufang
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, Ontario, K1S 5B6 and Université Lille 1 - Sciences et Technologies, UFR de Mathématiques, Laboratoire de Mathématiques Paul Painlevé - UMR CNRS 8524, 59655 Villeneuve d‘Ascq Cédex, France, e-mail: [email protected], [email protected]
Zhong-Jin Ruan
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study locally compact quantum groups $\mathbb{G}$ through the convolution algebras 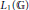${{L}_{1}}\left( \mathbb{G} \right)$ and 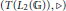$\left( T\left( {{L}_{2}}\left( \mathbb{G} \right) \right),\triangleright \right)$. We prove that the reduced quantum group 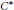${{C}^{*}}$ -algebra 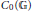${{C}_{0}}\left( \mathbb{G} \right)$ can be recovered from the convolution $\triangleright $ by showing that the right 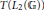$T\left( {{L}_{2}}\left( \mathbb{G} \right) \right)$-module 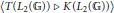$\left\langle K\left( {{L}_{2}}\left( \mathbb{G} \right) \right)\,\triangleright \,T\left( {{L}_{2}}\left( \mathbb{G} \right) \right) \right\rangle $ is equal to 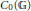${{C}_{0}}\left( \mathbb{G} \right)$. On the other hand, we show that the left 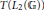$T\left( {{L}_{2}}\left( \mathbb{G} \right) \right)$-module 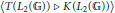$\left\langle T\left( {{L}_{2}}\left( \mathbb{G} \right) \right)\,\triangleright \,K\left( {{L}_{2}}\left( \mathbb{G} \right) \right) \right\rangle $ is isomorphic to the reduced crossed product 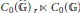${{C}_{0}}\left( \widehat{\mathbb{G}} \right){{\,}_{r}}\,\ltimes \,{{C}_{0}}\left( \mathbb{G} \right)$, and hence is a much larger 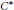${{C}^{*}}$ -subalgebra of 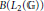$B\left( {{L}_{2}}\left( \mathbb{G} \right) \right)$.

We establish a natural isomorphism between the completely bounded right multiplier algebras of 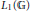${{L}_{1}}\left( \mathbb{G} \right)$ and 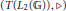$\left( T\left( {{L}_{2}}\left( \mathbb{G} \right) \right),\,\triangleright \right)$, and settle two invariance problems associated with the representation theorem of Junge–Neufang–Ruan (2009). We characterize regularity and discreteness of the quantum group $\mathbb{G}$ in terms of continuity properties of the convolution $\triangleright $ on 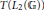$T\left( {{L}_{2}}\left( \mathbb{G} \right) \right)$. We prove that if $\mathbb{G}$ is semiregular, then the space 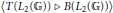$\left\langle T\left( {{L}_{2}}\left( \mathbb{G} \right) \right)\,\triangleright \,B\left( {{L}_{2}}\left( \mathbb{G} \right) \right) \right\rangle $ of right $\mathbb{G}$-continuous operators on 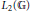${{L}_{2}}\left( \mathbb{G} \right)$, which was introduced by Bekka (1990) for 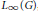${{L}_{\infty }}\left( G \right)$, is a unital 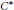${{C}^{*}}$-subalgebra of 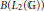$B\left( {{L}_{2}}\left( \mathbb{G} \right) \right)$. In the representation framework formulated by Neufang–Ruan–Spronk (2008) and Junge–Neufang–Ruan, we show that the dual properties of compactness and discreteness can be characterized simultaneously via automatic normality of quantum group bimodule maps on 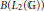$B\left( {{L}_{2}}\left( \mathbb{G} \right) \right)$. We also characterize some commutation relations of completely bounded multipliers of 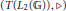$\left( T\left( {{L}_{2}}\left( \mathbb{G} \right) \right),\,\triangleright \right)$ over 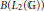$B\left( {{L}_{2}}\left( \mathbb{G} \right) \right)$.

Keywords

22D1543A3046H05locally compact quantum groups and associated Banach algebras
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 5 , 01 October 2013 , pp. 1043 - 1072
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] S. Baaj, , Représentation régulière du groupe quantique des déplacements de Woronowicz. Astérisque 232(1995), 11–48.Google Scholar
[2] Baaj, S. and Skandalis, G., Unitaires multiplicatifs et dualitépour les produits croisés de C*-algèbres. Ann. Sci. École Norm. Sup. (4) 26(1993), no. 4, 425–488.Google Scholar
[3] Baaj, S., Skandalis, G., and Vaes, S., Non-semi-regular quantum groups coming from number theory. Comm. Math. Phys. 235(2003), no. 1, 139–167. http://dx.doi.org/10.1007/s00220-002-0780-6 Google Scholar
[4] Bédos, E. and Tuset, L., Amenability and co-amenability for locally compact quantum groups. Internat. J. Math. 14(2003), no. 8, 865–884. http://dx.doi.org/10.1142/S0129167X03002046 Google Scholar
[5] Bekka, M. B., Amenable unitary representations of locally compact groups. Invent. Math. 100(1990), no. 2, 383–401.http://dx.doi.org/10.1007/BF01231192 Google Scholar
[6] Burnikel, C., Beschränkte Bimodulhomomorphismen über kommutativen Algebren und ihre Invarianzeigenschaften, Diploma Thesis, University of Saarland, Saarbrücken, Germany, 1992.Google Scholar
[7] Dales, H. G. and T.-M. Lau, A., The second duals of Beurling algebras. Mem. Amer. Math. Soc. 177(2005), no. 836.Google Scholar
[8] Effros, E. and Ruan, Z.-J., Discrete quantum groups. I. The Haar measure. Internat. J. Math. 5(1994), no. 5, 681–723. http://dx.doi.org/10.1142/S0129167X94000358 Google Scholar
[9] Granirer, E. E., Weakly almost periodic and uniformly continuous functionals on the Fourier algebra of any locally compact group. Trans. Amer. Math. Soc. 189(1974), 371–382. http://dx.doi.org/10.1090/S0002-9947-1974-0336241-0 Google Scholar
[10] Hofmeier, H. and Wittstock, G, A bicommutant theorem for completely bounded module homomorphisms. Math. Ann. 308(1997), no. 1, 141–154. http://dx.doi.org/10.1007/s002080050069 Google Scholar
[11] Hu, Z., Neufang, M., and Ruan, Z.-J.,On topological centre problems and SIN quantum groups. J. Funct. Anal. 257(2009), no. 2, 610–640. http://dx.doi.org/10.1016/j.jfa.2009.02.004 Google Scholar
[12] Hu, Z., Multipliers on a new class of Banach algebras, locally compact quantum groups, and topological centres. Proc. London Math. Soc. (3) 100(2010), no. 2, 429–458.http://dx.doi.org/10.1112/plms/pdp026 Google Scholar
[13] Hu, Z., Module maps on duals of Banach algebras and topological centre problems. J. Funct. Anal. 260(2011), no. 4, 1188–1218.http://dx.doi.org/10.1016/j.jfa.2010.10.017 Google Scholar
[14] Hu, Z., Completely bounded multipliers over locally compact quantum groups. Proc. London Math. Soc. 103(2011), no. 1, 1–39.http://dx.doi.org/10.1112/plms/pdq041 Google Scholar
[15] Hu, Z., Module maps over locally compact quantum groups. Studia Math., to appear.Google Scholar
[16] Junge, M., Neufang, M., and Ruan, Z.-J., A representation theorem for locally compact quantum groups. Internat. J. Math. 20(2009), no. 3, 377–400. http://dx.doi.org/10.1142/S0129167X09005285 Google Scholar
[17] Kustermans, J. and Vaes, S., Locally compact quantum groups. Ann. Sci. Éole Norm. Sup. 33(2000), no. 6, 837–934.Google Scholar
[18] Kustermans, J. Locally compact quantum groups in the von Neumann algebraic setting. Math. Scand. 92(2003), no. 1, 68–92.Google Scholar
[19] Lau, A. T.-M., Uniformly continuous functionals on Banach algebras Colloq. Math. 51(1987), 195–205.Google Scholar
[20] Mackey, G.W., A theorem of Stone and von Neumann. Duke Math. J. 16(1949), 313–326.http://dx.doi.org/10.1215/S0012-7094-49-01631-2 Google Scholar
[21] Neufang, M., Abstrakte Harmonische Analyse und Modulhomomorphismen über von Neumann-Algebren. Ph.D. thesis, University of Saarland, Saarbrücken, Germany, 2000.Google Scholar
[22] Neufang, M., Ruan, Z.-J., Spronk, N., Completely isometric representations of McbA(G) and UCB(Ĝ)*. Trans. Amer. Math. Soc. 360(2008), no. 3, 1133–1161. http://dx.doi.org/10.1090/S0002-9947-07-03940-2 Google Scholar
[23] Rosenberg, J., A selective history of the Stone-von Neumann theorem. In: Operator algebras, quantization, and noncommutative geometry, Contemp. Math., 365, American Mathematical Society, Providence, RI, 2004, pp. 331–353.Google Scholar
[24] Runde, V., Amenability for dual Banach algebras. Studia Math. 148(2001), no. 1, 47–66. http://dx.doi.org/10.4064/sm148-1-5 Google Scholar
[25] Runde, V., Characterizations of compact and discrete quantum groups through second duals. J. Operator Theory 60(2008), no. 2, 415–428.Google Scholar
[26] Runde, V., Uniform continuity over locally compact quantum groups. J. Lond. Math. Soc. 80(2009), no. 1, 55–71.http://dx.doi.org/10.1112/jlms/jdp011 Google Scholar
[27] Vaes, S., A new approach to induction and imprimitivity results. J. Funct. Anal. 229(2005), no. 2, 317–374.http://dx.doi.org/10.1016/j.jfa.2004.11.016 Google Scholar
[28] van Daele, A., Locally compact quantum groups. A von Neumann algebra approach. preprint, 2006.http://front.math.ucdavis.edu/0602.5212. Google Scholar