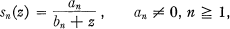Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jones, William B.
and
Snell, R. I.
1969.
Truncation Error Bounds for Continued Fractions.
SIAM Journal on Numerical Analysis,
Vol. 6,
Issue. 2,
p.
210.
Jones, William B.
and
Thron, W. J.
1970.
Twin-convergence regions for continued fractions 𝐾(𝑎_{𝑛}/1).
Transactions of the American Mathematical Society,
Vol. 150,
Issue. 1,
p.
93.
Field, David A.
and
Jones, William B.
1972.
A priori estimates for truncation error of continued fractionsK(1/b n ).
Numerische Mathematik,
Vol. 19,
Issue. 4,
p.
283.
Jones, William B.
and
Thron, W. J.
1974.
Numerical stability in evaluating continued fractions.
Mathematics of Computation,
Vol. 28,
Issue. 127,
p.
795.
Field, David A.
1978.
Error Bounds for Elliptic Convergence Regions for Continued Fractions.
SIAM Journal on Numerical Analysis,
Vol. 15,
Issue. 3,
p.
444.
Field, David A.
1978.
Error bounds for continued fractionsK(1/b n).
Numerische Mathematik,
Vol. 29,
Issue. 3,
p.
261.
Reid, Walter M.
1982.
Analytic Theory of Continued Fractions.
Vol. 932,
Issue. ,
p.
206.
Van Der Cruyssen, P.
1982.
Convergence of generalized continued fractions.
International Journal of Computer Mathematics,
Vol. 10,
Issue. 3-4,
p.
295.
Gragg, W. B.
and
Warner, D. D.
1983.
Two Constructive Results in Continued Fractions.
SIAM Journal on Numerical Analysis,
Vol. 20,
Issue. 6,
p.
1187.
Jacobsen, Lisa
and
Magnus, Arne
1984.
Rational Approximation and Interpolation.
Vol. 1105,
Issue. ,
p.
243.
JACOBSEN, LISA
and
WAADELAND, HAAKON
1986.
Numerical Mathematics and Applications.
p.
79.
Jacobsen, Lisa
and
Waadeland, Haakon
1988.
Convergence acceleration of limit periodic continued fractions under asymptotic side conditions.
Numerische Mathematik,
Vol. 53,
Issue. 3,
p.
285.
Jacobsen, Lisa
1990.
Computational Methods and Function Theory.
Vol. 1435,
Issue. ,
p.
89.
Lorentzen, Lisa
1995.
Computation of limit periodic continued fractions. A survey.
Numerical Algorithms,
Vol. 10,
Issue. 1,
p.
69.
Kuchmins'ka, Kh. I.
1998.
The element sets and value sets of two-dimensional continued fractions.
Journal of Mathematical Sciences,
Vol. 90,
Issue. 5,
p.
2368.
Zhao, Huan-xi
and
Zhu, Gongqin
2003.
Matrix-valued continued fractions.
Journal of Approximation Theory,
Vol. 120,
Issue. 1,
p.
136.
Lorentzen, Lisa
2003.
Plenary Papers A Priori Truncation Error Bounds for Continued Fractions.
Rocky Mountain Journal of Mathematics,
Vol. 33,
Issue. 2,
Bilanyk, I. B.
and
Bodnar, D. I.
2022.
Двовимірне узагальнення теореми Трона–Джоунса про параболічні множини збіжності неперервних дробів.
Ukrains’kyi Matematychnyi Zhurnal,
Vol. 74,
Issue. 9,
p.
1155.
Bilanyk, I. B.
and
Bodnar, D. I.
2023.
Two-Dimensional Generalization of the Thron–Jones Theorem on the Parabolic Domains of Convergence of Continued Fractions.
Ukrainian Mathematical Journal,
Vol. 74,
Issue. 9,
p.
1317.
Lukyanenko, Anton
and
Vandehey, Joseph
2024.
Convergence of improper Iwasawa continued fractions.
International Journal of Number Theory,
Vol. 20,
Issue. 02,
p.
299.