Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:55:55.100Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity of the Scattering Transformation for the Korteweg de Vries Equation

Published online by Cambridge University Press:  20 November 2018

Henri-François Gautrin  and
Tapio Klemola
Henri-François Gautrin
Affiliation:
University of Montreal, Montreal, Quebec
Tapio Klemola
Affiliation:
University of Montreal, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is at present well known that, if q(x, t) is a solution of the Korteweg de Vries (K d V) equation

(1)

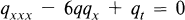
such that q(x, 0) = q0(x), where q0(x) behaves reasonably at infinity, and if

are the scattering data (see [4]) corresponding to q(x, t), then

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 2 , 01 April 1986 , pp. 360 - 375
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Ablowitz, M. J. and Segur, H., Solitons and the inverse scattering transform, SIAM (1981).CrossRefGoogle Scholar
2. Chadan, K. and Sabatier, P. C., Inverse problems in quantum scattering theory (Springer Verlag, 1977).CrossRefGoogle Scholar
3. Deift, P. and Trubowitz, E., Inverse scattering on the line, Comm. on pure and appl. Math. 32 (1979), 121.Google Scholar
4. Faddeev, L. D., Properties of the S-matrix of the one-dimensional Schroëdinger equation, Trusdy, mat. inst., Steklov 73 (1964), 314.Google Scholar
5. Montel, P., Leçons sur les familles normales de fonctions analytiques et leurs applications (Chelsea publishing company, New York, 1974).Google Scholar
6. Saks, S. and Zygmund, A., Analytic functions (Paristwewe Widawniscto Nankowe, Warsave, 1965).Google Scholar