Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-05T10:38:47.848Z Has data issue: false hasContentIssue false
  • English
  • Français

A Construction in General Radical Theory

Published online by Cambridge University Press:  20 November 2018

Augusto H. Ortiz
Augusto H. Ortiz*
Affiliation:
University of Puerto Rico, Mayaguez, Puerto Rico
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given an arbitrary associative ring R we consider the ring R[x] of polynomials over R in the commutative indeterminate x. For each radical property S we define the function S* which assigns to each ring R the ideal

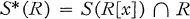
of R. It is shown that the property SA (that a ring R be equal to S*(R)) is a radical property. If S is semiprime, then SA is semiprime also. If S is a special radical, then SA is a special radical. SA is always contained in S. A necessary and sufficient condition that S and SA coincide is given.

The results are generalized in the last section to include extensions of R other than R[x], One such extension is the semigroup ring R[A], where A is a semigroup with an identity adjoined.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 6 , 01 December 1970 , pp. 1097 - 1100
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Amitsur, S. A., A general theory of radicals. II, Amer. J. Math. 76 (1954), 100–125.Google Scholar
2. Amitsur, S. A., Radicals of polynomial rings, Can. J. Math. 8 (1956), 355–361.Google Scholar
3. Divinsky, N. J., Rings and radicals (Univ. Toronto Press, Toronto, Ontario, 1965).Google Scholar
4. McCoy, N. H., The prime radical of a polynomial ring, Publ. Math. Debrecen 4 (1956), 161–162.Google Scholar
5. McCoy, N. H., Certain classes of ideals in polynomial rings, Can. J. Math. 9 (1957), 352–362.Google Scholar
6. Nagata, M., On the theory of radicals in a ring, J. Math. Soc. Japan 3 (1951), 330–344.Google Scholar