Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-21T13:19:55.982Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructing Representations of Finite Simple Groups and Covers

Published online by Cambridge University Press:  20 November 2018

Vahid Dabbaghian-Abdoly
Vahid Dabbaghian-Abdoly*
Affiliation:
Centre for Experimental and Constructive Mathematics, Simon Fraser University, 8888 University Drive, Burnaby, BC V5A 1S6 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 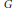$G$ be a finite group and $\chi $ be an irreducible character of 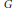$G$. An efficient and simple method to construct representations of finite groups is applicable whenever 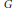$G$ has a subgroup 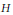$H$ such that 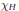$\chi H$ has a linear constituent with multiplicity 1. In this paper we show (with a few exceptions) that if 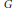$G$ is a simple group or a covering group of a simple group and $\chi $ is an irreducible character of 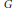$G$ of degree less than 32, then there exists a subgroup 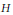$H$ (often a Sylow subgroup) of 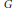$G$ such that 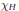$\chi H$ has a linear constituent with multiplicity 1.

Keywords

20C4020C1group representationssimple groupscentral coversirreducible representations
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 1 , 01 February 2006 , pp. 23 - 38
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A., and Wilson, R. A., Atlas of Finite Groups. Maximal Subgroups and Ordinary Characters for Simple Groups. Oxford University Press, Oxford, 1985.Google Scholar
[2] Atlas of Finite Group Representations. School of Mathematics and Statistics, The University of Birmingham, Version 2, http://web.mat.bham.ac.uk/atlas/v2.0/. Google Scholar
[3] Dabbaghian-Abdoly, V., An Algorithm to Construct Representations of Finite Groups. Ph.D. thesis, School of Mathematics, Carleton University, 2003.Google Scholar
[4] Dabbaghian-Abdoly, V., REPSN - A Package for Constructing Representations of Finite Groups. GAP package. http://www.gap_system.org/Packages/repsn.html 2004.Google Scholar
[5] Dixon, J. D., Constructing representations of finite groups. In: Groups and Computation, DIMACS Ser. Discrete Math. Theoret. Comput. Sci. 11, American Mathematical Society, Providence, RI, 1993, pp. 105–112.Google Scholar
[6] Dornhoff, L., Group Representation Theory. Part A: Ordinary Representation Theory. Pure and Applied Mathematics 7, Marcel Dekker, New York, 1971.Google Scholar
[7]The GAP Group, GAP–Groups, Algorithms, Programming–A System for Computation Discrete Algebra. Version 4.3, 2002, http://www.gap-system.org. Google Scholar
[8] James, G. and Kerber, A., The Representation Theory of the Symmetric Group. Encyclopedia of Mathematics and its Applications 16, Addison-Wesley, London, 1981.Google Scholar
[9] Janusz, G. J., Primitive idempotents in group algebras. Proc. Amer.Math. Soc. 17(1966), 520–523.Google Scholar
[10] Gorenstein, D., Lyons, R., and Solomon, R., The Classification of the Finite Simple Groups: Almost Simple K-groups. Mathematical Surveys and Monographs 40.3, American Mathematical Society, Providence, RI, 1998.Google Scholar
[11] Güzel, E., Les représentations irréductibles complexes des groups SL(3, q), PSL(3, q). J. Karadeniz Tech. Univ. Fac. Arts Sci. Ser.Math.-Phys. 11(1988), 53–62.Google Scholar
[12] Isaacs, I. M., Character Theory of Finite Groups. Corrected reprint of the 1976 original. Dover, New York, 1994.Google Scholar
[13] Karpilovsky, G., The Schur Multiplier. London Mathematical Society Monographs 2, Oxford University Press, New York, 1987.Google Scholar
[14] Simpson, A.W. and Frame, J. S., The character tables for SL(3, q), SU(3, q2), PSL(3, q), PSU(3, q2). Canad. J. Math. 25(1973), 486–494.Google Scholar