Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T21:46:02.273Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruence Subgroups of the Picard Group

Published online by Cambridge University Press:  20 November 2018

Benjamin Fine
Benjamin Fine*
Affiliation:
Fairfield University, Fairfield, Connecticut
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Picard group Γ = PSL2 (Z [i]) is the group of linear fractional transformations

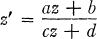
with ad – bc = ± 1 and a, b, c, d Gaussian integers.

Γ is of interest as an abstract group and in automorphic function theory. In an earlier paper [1], a decomposition of Γ as a free product with amalgamated subgroup was given and this was utilized to investigate Fuchsian subgroups. Karrass and Solitar used a similar decomposition to characterize abelian and nilpotent subgroups. Maskit [6], Mennicke [7] and Fine [2], used Γ to generate faithful representations of Fundamental Groups of Riemann Surfaces while more recently Wielenberg [10] represented certain knot and link groups as subgroups of Γ. In this paper, we will examine the structure of the congruence subgroups of Γ. Our technique will be to use the decomposition cited above [1], together with the Karrass-Solitar subgroup structure theory for free products with amalgamations [3]. Finally, we give a conjecture and some results concerning Fuchsian subgroups which are contained in congruence subgroups.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 6 , 01 December 1980 , pp. 1474 - 1481
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Fine, B., Fuchsian subgroups of the Picard group, Can. J. Math. 28 (1976), 481–485.Google Scholar
2. Fine, B., The structure of PSL2(R), Annals of Mathematics, Study 79 on Discontinuous Groups and Riemann Surface (1974).Google Scholar
3. Karrass, A. and Solitar, D., The subgroups of a free product of two groups with an amalgamated subgroup, Trans. Amer. Math. Soc. 150 (1970), 227–255.Google Scholar
4. Lehner, J., Discontinuous groups and automorphic functions, Math Surveys No. 8, Amer. Math. Soc. (Providence, R.I., 1964).CrossRefGoogle Scholar
5. Magnus, W., Karrass, A. and Solitar, D., Combinatorial group theory (Interscience, Wiley, New York, 1966).Google Scholar
6. Maskit, B., On a class of Kleinian groups, Ann. Academia Scient. Fennical, I. Mathematica, Helsinki (1969), 1–7.Google Scholar
7. Mennicke, J., A note on regular coverings of closed orientable surfaces, Proc. Glasgow Math. Assoc. 5 (1969), 49–66.Google Scholar
8. Newman, M., Integral matrices (Academic Press, N.Y., 1972).Google Scholar
9. Waldinger, H., On the subgroups of the Picard group, Proc. Amer. Math. Soc. 16 (1965), 1375–1378.Google Scholar
10. Wielenberg, N., The structure of certain subgroups of the Picard group (to appear in Univ. of Pittsburgh Press).CrossRefGoogle Scholar