Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T19:58:00.849Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruence Representations in Algebraic Number Fields II. Simultaneous Linear and Quadratic Congruences

Published online by Cambridge University Press:  20 November 2018

Eckford Cohen
Eckford Cohen*
Affiliation:
University of Tennessee
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ƒ and λ be positive integers and p a positive odd prime. Suppose further that P is an ideal of norm pf in a finite extension F of the rational field. In (2), which will also be referred to as I in the present paper, we obtained the number of solutions Ns(m) of the quadratic congruence,

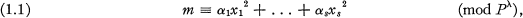
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 10 , 1958 , pp. 561 - 571
Copyright
Copyright © Canadian Mathematical Society 1958

References

1. Carlitz, Leonard, Weighted quadratic partitions (mod pr), Math. Z., 59 (1953), 40-46.Google Scholar
2. Cohen, Eckford, Congruence representations in algebraic number fields, Trans. Amer. Math. Soc, 75 (1953), 444-470.Google Scholar
3. Cohen, Eckford, Simultaneous pairs of linear and quadratic equations in a Galois field, Can. J. Math., 9 (1957), 74-78.Google Scholar
4. Hecke, Erich, Vorlesungen ueber die Theorie der algebraischen Zahlen (Leipzig, 1923).Google Scholar
5. O'Connor, R. E., Quadratic and linear congruence, Bull. Amer. Math. Soc, 45.(1939), 792-798.Google Scholar