Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:30:33.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Compositions of Set Operations

Published online by Cambridge University Press:  20 November 2018

D. W. Bressler  and
A. H. Cayford
D. W. Bressler
Affiliation:
Sacramento State College, Sacramento, California
A. H. Cayford
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The set operations under consideration are Borel operations and Souslin's operation (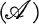). With respect to a given family of sets and in a setting free of any topological structure there are defined three Borel families (Definitions 3.1) and the family of Souslin sets (Definition 4.1). Conditions on an initial family are determined under which iteration of the Borel operations with Souslin's operation (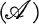) on the initial family and the families successively produced results in a non-decreasing sequence of families of analytic sets (Theorem 5.2.1 and Definition 3.5). A classification of families of analytic sets with respect to an initial family of sets is indicated in a manner analogous to the familiar classification of Borel sets (Definition 5.3).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 2 , 01 April 1970 , pp. 227 - 234
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Bressler, D. W. and Sion, M., The current theory of analytic sets, Can. J. Math. 16 (1964), 207–230.Google Scholar
2. Kuratowski, C., Les suites transfinies d'ensembles et les ensembles projectifs, Fund. Math. 28 (1937), 186–195.Google Scholar
3. Lusin, N., Sur la classification de M. Baire, C. R. Acad. Sci. Paris 164 (1917), 91–94.Google Scholar
4. Lusin, N., Sur les ensembles analytiques, Fund. Math. 10 (1927), 1–95.Google Scholar
5. Lusin, N. and Sierpinski, W., Sur quelques proprieties des ensembles (), Bull. Acad. Sci. Cracovie 1918, 37–48.Google Scholar
6. Morse, A. P., The role of internal families in measure theory. Bull. Amer. Math. Soc. 50 (1944), 723–728.Google Scholar
7. Sierpinski, W., Les ensembles boreliens abstraits, Ann. Soc. Polon. Math. 6 (1927), 50–53.Google Scholar
8. Souslin, M., Sur une definition des ensembles mesurables B sans nombres transfinis, C. R. Acad. Sci. Paris 164 (1917), 88–91.Google Scholar