Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:07:56.949Z Has data issue: false hasContentIssue false
  • English
  • Français

A Compactification with θ-Continuous Lifting Property

Published online by Cambridge University Press:  20 November 2018

D. C. Kent  and
G. D. Richardson
D. C. Kent
Affiliation:
Washington State University, Pullman, Washington
G. D. Richardson
Affiliation:
East Carolina University, Greenville, North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

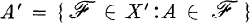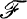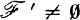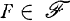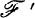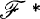1. Let X be a topological space, and let X′ be the set of all non-convergent ultrafilters on X. If A ⊆ X, let , and A* = A ∪ A′. If is a filter on X such that for all , then let. be the filter on X* generated by ; let be the filter on X* generated by 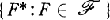. If 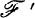exists then 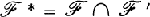; otherwise, .

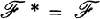A convergence is defined on X* as follows: If x ∈ X, then a filter A → x in X* if and only if 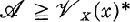, where Vx(x) is the X neighborhood filter at x; 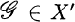, then 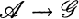in X* if and only if .

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 6 , 01 December 1982 , pp. 1330 - 1334
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Dickman, R. F. and Porter, J. R., 0-perfect and O-absolutely closed functions, Ill. J. Math. 21 (1977), 42–60.Google Scholar
2. Gazik, R. J., Regularity of Richardson s compactification, Can. J. Math. 26 (1974), 1289–1293.Google Scholar
3. Richardson, G. D., A Stone-Cech compactification for limit spaces, Proc. Amer. Math. Soc. 25 (1970), 403–404.Google Scholar