Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:42:10.298Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact Operators in Reductive Algebras

Published online by Cambridge University Press:  20 November 2018

Edward A. Azoff
Edward A. Azoff*
Affiliation:
University of Georgia, Athens, Georgia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 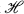be a Hilbert space and denote the collection of (bounded, linear) operators on 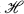by 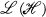. Throughout this paper, the term ‘algebra’ will refer to a subalgebra of 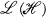; unless otherwise stated, it will not be assumed to contain I or to be closed in any topology.

An algebra is said to be transitive if it has no non-trivial invariant subspaces. The following lemma has revolutionized the study of transitive algebras. For a pr∞f and a general discussion of its implications, the reader is referred to [5].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 1 , 01 February 1975 , pp. 152 - 154
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Cater, F. S., Lectures on real and complex vector spaces (W. B. Saunders Co., Philadelphia, 1966).Google Scholar
2. Dixmier, J., Les algebres d'operateurs dans Vespace Hilbertien, 2nd edition (Gauthier-Villars, Paris, 1969).Google Scholar
3. Gamelin, T., Uniform algebras (Prentice Hall, Englew∞d, N.J., 1969).Google Scholar
4. Gilfeather, F., On the Suzuki structure theory for non self-adjoint operators on Hilbert space, Acta Sci. Math. (Szeged) 32 (1971), 239–249.Google Scholar
5. Pearcy, C. and Shields, A., A survey of the Lomonosov technique in the theory of invariant subspaces, Topics in Operator Theory, Math. Surveys, No. 13 (Amer. Math. Soc, Providence, 1974).Google Scholar
6. Radjavi, H. and Rosenthal, P., A sufficient condition that an operator algebra be self-adjoint, Can. J. Math., 23 (1971), 588–597.Google Scholar
7. Rosenthal, P., On reductive algebras containing compact operators (to appear in Proc. Amer. Math. Soc).Google Scholar