Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:16:45.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Collineations of Affine Moulton Planes

Published online by Cambridge University Press:  20 November 2018

William A. Pierce
William A. Pierce*
Affiliation:
Syracuse University Syracuse 10, New York, and West Virginia University Morgantown, West Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent article on Moulton planes (8), I have generalized the non-Desarguesian planes introduced by F. R. Moulton (6) and Pickert (7, pp. 93-94). Let F = (0, 1; a, b, . . . , x, y, . . .} denote a given field, having P as a multiplicative subgroup of index 2. Define x > 0 or x < 0 according as x lies in P or in the other coset of non-zero elements. The function ϕ is order-preserving, and can be assumed to satisfy ϕ(0) = 0, ϕ(1) = 1. For any n < 0, the maps x —> ϕ(x) and x —> ϕ(x) — nx both carry F onto itself. The elements of F form a Cartesian group, {+,0} being defined so that

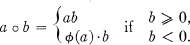
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 16 , 1964 , pp. 46 - 62
Copyright
Copyright © Canadian Mathematical Society 1964

References

1. André, J., Projektive Ebenen über Fastkörpern, Math. Zeit., 62 (1955), 137–160.Google Scholar
2. Barlotti, A., Le possibili configurazioni del sistema delle coppie punto-retta (A, a) per cui un piano grafico risulta (A, a) transitive, Boll. Un. Mat. Italiano, 12 (1957), 212–226.Google Scholar
3. Carlitz, L., A theorem on permutations in a finite field, Proc. Amer. Math. Soc, 11 (1960), 456–459.Google Scholar
4. Hall, M. Jr., Projective planes, Trans. Amer. Math. Soc, 54 (1943), 229–277.Google Scholar
5. Lenz, H., Kleiner desarguesscher Satz und Dualitàt in projektiven Ebenen, Jahresber. Deutscher Math. Verein, 57 (1954), 20–31.Google Scholar
6. Moulton, F. R., A simple non-Desarguesian plane, Trans. Amer. Math. Soc, 3 (1902), 192–195.Google Scholar
7. Pickert, G., Projektive Ebenen, (Berlin, 1955).Google Scholar
8. Pierce, W. A., Moulton planes, Can. J. Math., 13 (1961), 427–436. (corrected in the Appendix of the present paper).Google Scholar
9. Spencer, J. C. D., On the Lenz-Barlotti classification of projective planes, Quart. J. Math., 2 (1960), 241–257.Google Scholar
10. Veblen, O. and Wedderburn, J. H. M., Non-Desarguesian and non-Pascalian geometries, Trans. Amer. Math. Soc, 8 (1907), 379–388.Google Scholar
11. Zassenhaus, H., Über endliche Fastkörper, Abh. Math. Sem. Univ. Hamburg, 11 (1936), 187–220.Google Scholar