Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:40:46.380Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficients of Symmetric Functions of Bounded Boundary Rotation

Published online by Cambridge University Press:  20 November 2018

Ronald J. Leach
Ronald J. Leach*
Affiliation:
Howard University, Washington, D.C.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

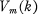Let denote the family of all functions of the form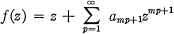

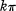that are analytic in the unit disc U, f′(z) ≠ 0 in U and f maps U onto a domain of boundary rotation at most . Recently Brannan, Clunie and Kirwan [2] and Aharonov and Friedland [1] have solved the problem of estimating |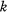amp+1| for all , provided m = 1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 6 , December 1974 , pp. 1351 - 1355
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Aharonov, D. and Friedland, S. (to appear).Google Scholar
2. Brannan, D., Clunie, J., and Kirwan, W., On the coefficient problem for functions of bounded boundary rotation (to appear).Google Scholar
3. Brannan, D., On functions of bounded boundary rotation, Proc. Edinburgh Math. Soc. 16 (1968-9), 339–347.Google Scholar
4. Hayman, W., Multivalent functions (Cambridge Univ. Press, Cambridge, 1958).Google Scholar
5. Leach, R., On odd functions of bounded boundary rotation, Can. J. Math, (to appear).Google Scholar
6. Lehto, O., On the distortion of conformai mappings with bounded boundary rotation, Ann. Acad. Sci. Fenn. Ser. A 1 Math. Phys. 124 (1952), 14 pp.Google Scholar
7. Noonan, J., On close-to-convex functions of order β, Pacific J. Math, (to appear).Google Scholar
8. Noonan, J., Asymptotic behavior of functions with bounded boundary rotation, Trans. Amer. Math. Soc. 164 (1972), 397–416.Google Scholar
9. Umezawa, T., On the theory of univalent functions, Tôhoku Math. J. 7 (1955), 212–223.Google Scholar