Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-19T11:01:14.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficient Behavior of a Class of Meromorphic Functions

Published online by Cambridge University Press:  20 November 2018

J. W. Noonan
J. W. Noonan*
Affiliation:
Holy Cross College Worcester, Massachusetts
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

With 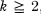, denote by Λk the class of functions ƒ of the form

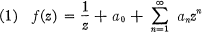
which are analytic in 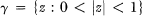and which map y onto the complement of a domain with boundary rotation at most 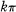. It is known [2] that ƒ ∈ Λk if and only if there exist regular starlike functions s1 and s2, with

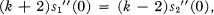
such that

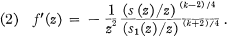
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 5 , 01 October 1975 , pp. 1157 - 1165
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Hille, E., Analytic function theory, Vol. II (Ginn, Boston, 1962).Google Scholar
2. Noonan, J. W., Meromorphic functions of bounded boundary rotation, Michigan Math. J. 18 (1971), 343–352.Google Scholar
3. Noonan, J. W., Asymptotic behavior of functions with bounded boundary rotation, Trans. Amer. Math. Soc. 164 (1972), 397–410.Google Scholar
4. Noonan, J. W., On close-to-convex functions of order 0, Pacific J. Math. 44 (1973), 263–280.Google Scholar
5. Noonan, J. W., Curvature and radius of curvature for functions with bounded boundary rotation, Can. J. Math. 25 (1973), 1015–1023.Google Scholar
6. Pommerenke, Ch., On starlike and convex functions, J. London Math. Soc. 37 (1962), 209–224.Google Scholar
7. Pommerenke, Ch., On close-to-convex analytic functions, Trans. Amer. Math. Soc. 114 (1965), 176–186.Google Scholar
8. Thomas, D. K., On the coefficients of functions with bounded boundary rotation, Proc. Amer. Math. Soc. 36 (1972), 123–129.Google Scholar