Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Anderson, Tim
and
Kleinfeld, Erwin
1978.
On a class of 2-varieties.
Journal of Algebra,
Vol. 51,
Issue. 2,
p.
367.
Anderson, Tim
and
Gardner, B.J.
1978.
Semi-simple classes in a variety satisfying an Andrunakievich Lemma.
Bulletin of the Australian Mathematical Society,
Vol. 18,
Issue. 2,
p.
187.
Bakhturin, Yu. A.
Slin'ko, A. M.
and
Shestakov, I. P.
1982.
Nonassociative rings.
Journal of Soviet Mathematics,
Vol. 18,
Issue. 2,
p.
169.
Liu, Shao-Xue
and
Tsai, Chester E
1982.
Wedderburn theorem on varieties of algebras.
Journal of Algebra,
Vol. 75,
Issue. 2,
p.
315.
Hefendehl-Hebeker, Lisa
1983.
Zur Struktur der vierdimensionalen quadratischen Algebren.
Manuscripta Mathematica,
Vol. 41,
Issue. 1-3,
p.
173.
Roy Hentzel, Irvin
and
Maria Piacentini Cattaneo, Giulia
1984.
Degree three identities.
Communications in Algebra,
Vol. 12,
Issue. 19,
p.
2349.
Cattaneo, Giulia Maria Piacentini
1985.
A special class of 2-varieties.
Journal of Algebra,
Vol. 95,
Issue. 1,
p.
116.
Cattaneo, Giulia Maria Piacentini
1985.
A method for recognizing certain varieties of nonassociative algebras.
Journal of Algebra,
Vol. 97,
Issue. 2,
p.
347.
Gardner, B. J.
1992.
Strong semi-simplicity.
Periodica Mathematica Hungarica,
Vol. 24,
Issue. 1,
p.
23.


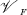 of power-associative algebras over a field
of power-associative algebras over a field 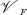 and each ideal I of
and each ideal I of 