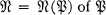Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fryer, K. D.
1955.
Note on permutations in a finite field.
Proceedings of the American Mathematical Society,
Vol. 6,
Issue. 1,
p.
1.
Parker, E. T.
and
Nikolai, Paul J.
1958.
A search for analogues of the Mathieu groups.
Mathematics of Computation,
Vol. 12,
Issue. 61,
p.
38.
Ito, Noboru
1963.
Transitive permutation groups of degree 𝑝=2𝑞+1,𝑝 and 𝑞 being prime numbers.
Bulletin of the American Mathematical Society,
Vol. 69,
Issue. 2,
p.
165.
Itô, Noboru
1965.
Transitive permutation groups of degree 𝑝=2𝑞+1,𝑝 and 𝑞 being prime numbers. III.
Transactions of the American Mathematical Society,
Vol. 116,
Issue. 0,
p.
151.
Shaughnessy, Edward P.
1971.
Codes with simple automorphism groups.
Archiv der Mathematik,
Vol. 22,
Issue. 1,
p.
459.
1973.
Algebra of Polynomials.
Vol. 5,
Issue. ,
p.
300.
Neumann, Peter M.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
520.
Neumann, Peter M.
1974.
Proceedings of the Second International Conference on the Theory of Groups.
Vol. 372,
Issue. ,
p.
520.
Ward, Harold N
1975.
A form for M11.
Journal of Algebra,
Vol. 37,
Issue. 2,
p.
340.
Ding, Zhiguo
2020.
Connecting two types of representations of a permutation of Fq.
Discrete Mathematics,
Vol. 343,
Issue. 4,
p.
111793.
Hakuta, Keisuke
2022.
Semilinear groups contained in alternating group on a finite-dimensional linear space.
Journal of Discrete Mathematical Sciences and Cryptography,
p.
1.


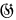 of finite order
of finite order  is a
is a