Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:02:12.923Z Has data issue: false hasContentIssue false
  • English
  • Français

Class Numbers and Biquadratic Reciprocity

Published online by Cambridge University Press:  20 November 2018

Kenneth S. Williams  and
James D. Currie
Kenneth S. Williams
Affiliation:
Carleton University, Ottawa, Ontario
James D. Currie
Affiliation:
Carleton University, Ottawa, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

0. Notation. Throughout this paper p denotes a prime congruent to 1 modulo 4. It is well known that such primes are expressible in an essentially unique manner as the sum of the squares of two integers, that is,

(0.1)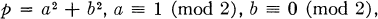

with |a| and |b| uniquely determined by (0.1). Since a is odd, replacing a by –a if necessary, we can specify a uniquely by

(0.2)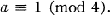

Further, as {[(p – l)/2]!}2 = – 1 (mod p), we can specify b uniquely by

(0.3)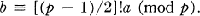

These choices are assumed throughout.

The following notation is also used throughout the paper: h(d) denotes the class number of the quadratic field 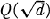of discriminant d, (d/n) is the Kronecker symbol of modulus |d|, [x] denotes the greatest integer less than or equal to the real number x, and {x} = x – [x].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 4 , 01 August 1982 , pp. 969 - 988
Copyright
Copyright © Canadian Mathematical Society 1982

References

References>

1. Berndt, B. C., Classical theorems on quadratic residues, L'Enseign. Math. 22 (1976), 261–304.Google Scholar
2. Borevich, Z. I. and Shafarevich, I. R., Number theory (Academic Press, N.Y., 1966).Google Scholar
3. P. G. L., Dirichlet, Recherches sur diverses applications de Vanalyse infinitésimale à la théorie des nombres, J. Reine Angew. Math. 21 (1840), 134–155.Google Scholar
4. Gauss, C. F., Letter to P. G. L. Dirichlet dated 30 May 1828. (Reproduced in P. G. L. Dirichlet's Werke, Chelsea Publishing Company, Bronx, N.Y. Volume 2, pp. 378–380.)Google Scholar
5. Gosset, T., On the law of quartic reciprocity, Mess. Math. 41 (1911), 65–90.Google Scholar
6. Johnson, W. and Mitchell, K. J., Symmetries for sums of the Legendre symbol, Pacific J. Math. 69 (1977), 117–124.Google Scholar
7. Kaplan, P., Sur le 2-groupe des classes d'idéaux des corps quadratiques, J. Reine Angew. Math. 283/284 (1976), 313–363.Google Scholar
8. Lehmer, E., On Euler's criterion, J. Austral. Math. Soc. 1 (1959), 64–70.Google Scholar
9. Pizer, A., On the 2-part of the class number of imaginary quadratic number fields, J. Number Theory 8 (1976), 184–192.Google Scholar
10. Yamamoto, K., On Gaussian sums with biquadratic residue characters, J. Reine Angew. Math. 219 (1965), 200–213.Google Scholar