Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Carlitz, L.
1961.
A generalization of Maillet’s determinant and a bound for the first factor of the class number.
Proceedings of the American Mathematical Society,
Vol. 12,
Issue. 2,
p.
256.
Uchida, Kôji
1971.
Class numbers of imaginary abelian number fields, II.
Tohoku Mathematical Journal,
Vol. 23,
Issue. 2,
Uchida, Kôji
1971.
Class numbers of imaginary abelian number fields, I.
Tohoku Mathematical Journal,
Vol. 23,
Issue. 1,
Goldstein, Larry Joel
1973.
On the class numbers of cyclotomic fields.
Journal of Number Theory,
Vol. 5,
Issue. 1,
p.
58.
Ribenboim, P.
1977.
Lecture—Recent Results on Fermat's Last Theorem.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 2,
p.
229.
Ribenboim, Paulo
1979.
13 Lectures on Fermat’s Last Theorem.
p.
19.
Ewing, John
1979.
The image of the Atiyah-Bott map.
Mathematische Zeitschrift,
Vol. 165,
Issue. 1,
p.
53.
Ribenboim, Paulo
1979.
13 Lectures on Fermat’s Last Theorem.
p.
115.
1989.
Topics in Field Theory.
Vol. 155,
Issue. ,
p.
477.
Katsurada, Masanori
and
Matsumoto, Kohji
1994.
The mean values of Dirichlet L-functions at integer points and class numbers of cyclotomic fields.
Nagoya Mathematical Journal,
Vol. 134,
Issue. ,
p.
151.
Ribenboim, Paulo
2001.
Classical Theory of Algebraic Numbers.
p.
639.
Murty, M.Ram
and
Petridis, Yiannis N
2001.
On Kummer's Conjecture.
Journal of Number Theory,
Vol. 90,
Issue. 2,
p.
294.
MYERS, M. J. R.
2010.
A GENERALISED KUMMER'S CONJECTURE.
Glasgow Mathematical Journal,
Vol. 52,
Issue. 3,
p.
453.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
369.
Moree, Pieter
2018.
Irregularities in the Distribution of Prime Numbers.
p.
143.


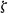 ), where
), where