Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T14:10:23.953Z Has data issue: false hasContentIssue false
  • English
  • Français

The Choquet–Deny Equation in a Banach Space

Published online by Cambridge University Press:  20 November 2018

Wojciech Jaworski  and
Matthias Neufang
Wojciech Jaworski
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON, K1S 5B6 email: [email protected], [email protected]
Matthias Neufang
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON, K1S 5B6 email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 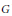$G$ be a locally compact group and $\pi $ a representation of 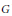$G$ by weakly* continuous isometries acting in a dual Banach space 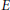$E$. Given a probability measure 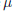$\mu $ on 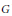$G$, we study the Choquet–Deny equation 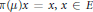$\pi (\mu )x\,=\,x,\,x\,\in \,E$. We prove that the solutions of this equation form the range of a projection of norm 1 and can be represented by means of a “Poisson formula” on the same boundary space that is used to represent the bounded harmonic functions of the random walk of law 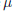$\mu $. The relation between the space of solutions of the Choquet–Deny equation in 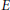$E$ and the space of bounded harmonic functions can be understood in terms of a construction resembling the 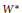${{W}^{*}}$-crossed product and coinciding precisely with the crossed product in the special case of the Choquet–Deny equation in the space 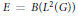$E\,=\,B({{L}^{2}}(G))$ of bounded linear operators on 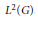${{L}^{2}}(G)$. Other general properties of the Choquet–Deny equation in a Banach space are also discussed.

Keywords

22D1222D2043A0560B1560J50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 4 , 01 August 2007 , pp. 795 - 827
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Adams, S., Elliott, G. A., and Giordano, T., Amenable actions of groups. Trans. Amer. Math. Soc. 344(1994), no. 2, 803–822.Google Scholar
[2] Anantharaman-Delaroche, C., Action moyennable d’un groupe localement compact sur une algèbre de von Neumann. Math. Scand. 45(1979), no. 2, 289–304.Google Scholar
[3] Anantharaman-Delaroche, C., Action moyennable d’un groupe localement compact sur une algèbre de von Neumann. II. Math. Scand. 50(1982), no. 2, 251–268.Google Scholar
[4] Azencott, R., Espaces de Poisson des groupes localement compacts. Lecture Notes in Mathematics 148, Springer-Verlag, Berlin, 1970.Google Scholar
[5] Chu, C.-H. and Lau, A. T., Harmonic functions on groups and Fourier algebras. Lecture Notes in Mathematics 1782, Springer-Verlag, Berlin 2002.Google Scholar
[6] Connes, A. and Woods, E. J., Approximately transitive flows and ITPFI factors. Ergodic Theory Dynam. Systems 5(1985), no. 2, 203–236.Google Scholar
[7] Connes, A. and Woods, E. J., Hyperfinite von Neumann algebras and Poisson boundaries of time dependent random walks. Pacific J. Math. 137(1989), no. 2, 225–243.Google Scholar
[8] Dunford, N. and Schwartz, J. T., Linear Operators. I. Wiley, New York 1988.Google Scholar
[9] Derriennic, Y., Lois “zéro ou deux” pour les processus de Markov. Applications aux marches aléatoires. Ann. Inst. H. Poincaré Sect. B (N.S.) 12(1976), no. 2, 111–129.Google Scholar
[10] Furstenberg, H., Boundary theory and stochastic processes on homogeneous spaces. In: Harmonic Analysis on Homogeneous Spaces, Proc. Sympos. Pure Math. 26. American Mathematical Society, Providence, RI, 1973, pp. 193–229.Google Scholar
[11] Furstenberg, H., Random walks and discrete subgroups of Lie groups. Advances in Probability and Related Topics 1, Dekker, 1971, pp. 3–63.Google Scholar
[12] Guivarc’h, Y., Extension d’un théorème de Choquet-Deny à une classe de groupes non abéliens. Astérisque 4, Soc. Math. France, Paris, 1973, pp. 41–59.Google Scholar
[13] Hewitt, E. and Savage, L. J., Symmetric measures on Cartesian products. Transactions Amer. Math. Soc. 80(1955), 470–501.Google Scholar
[14] Izumi, M., Non-commutative Poisson boundaries. Contemp. Math. 347(2004), 69–81.Google Scholar
[15] Jaworski, W., Poisson and Furstenberg Boundaries of Random Walks. Ph.D. Thesis, Queen's University, 1991.Google Scholar
[16] Jaworski, W., Poisson and Furstenberg boundaries of random walks. C. R. Math. Rep. Acad. Sci. Canada 13(1991), no. 6, 279–284.Google Scholar
[17] Jaworski, W., Countable amenable identity excluding groups. Canad. Math. Bull. 47(2004)), no. 2, 215–228.Google Scholar
[18] Jaworski, W., Probability measures on almost connected amenable locally compact groups and some related ideals in group algebras. Illinois J. Math. 45(2001), no. 1, 195–212.Google Scholar
[19] Jaworski, W., Ergodic and mixing probability measures on [SIN] groups. J. Theoret. Probab. 17(2004), 741–759.Google Scholar
[20] Jaworski, W., The asymptoti σ-algebra of a recurrent random walk on a locally compact group. Israel J. Math. 94(1996), 201–219.Google Scholar
[21] Jaworski, W., Strongly approximately transitive group actions, the Choquet-Deny theorem, and polynomial growth. Pacific J. Math. 165(1994), no. 1, 115–129.Google Scholar
[22] Jaworski, W., Strong approximate transitivity, polynomial growth, and spread out random walks on locally compact groups. Pacific J. Math. 170(1995), no. 2, 517–533.Google Scholar
[23] Jaworski, W., A Poisson formula for solvable Lie groups. J. Anal. Math. 68(1996), 183–208.Google Scholar
[24] Jaworski, W., Random walks on almost connected locally compact groups: boundary and convergence. J. Anal. Math. 74(1998), 235–273.Google Scholar
[25] Kaimanovich, V. A., The Poisson boundary of polycyclic groups. In: Probability Measures on Groups and Related Structures XI. World Sci. Publ., River Edge, NJ, 1995 pp. 182–195.Google Scholar
[26] Kaimanovich, V. A., The Poisson formula for groups with hyperbolic properties. Ann. of Math. 152(2000), no. 3, 659–692.Google Scholar
[27] Kaimanovich, V. A. and Vershik, A. M., Random walks on discrete groups: boundary and entropy. Ann. Probab. 11(1983), no. 3, 457–490.Google Scholar
[28] Ledrappier, F., Some asymptotic properties of random walks on free groups. In: Topics in Probability and Lie Groups: Boundary Theory. CRM Proc. Lecture Notes 28, American Mathematical Society. Providence, RI, 2001 pp. 117–152,.Google Scholar
[29] Mackey, G. W., Point realizations of transformation groups. Illinois J. Math. 6(1962), 327–335.Google Scholar
[30] Meyer, P.-A., Probabilités et potentiel. Hermann, Paris, 1966.Google Scholar
[31] Mukherjea, A., Limit theorems for probability measures on non-compact groups and semigroups. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 33(1975/1976), no. 4, 273–284.Google Scholar
[32] Neufang, M., Abstrakte harmonische Analyse und Modulhomomorphismen Über von Neumann-Algebren. Ph.D. Thesis, Universität des Saarlandes, 2000.Google Scholar
[33] Neufang, M., A quantized analogue of the convolution algebra L 1(G). Preprint, http://mathstat.carleton.ca/∼mneufang Google Scholar
[34] Neveu, J., Mathematical Foundations of the Calculus of Probability. Holden-Day, San Francisco, 1965.Google Scholar
[35] Neveu, J., Discrete-Parameter Martingales. North-Holland, Amsterdam, 1975.Google Scholar
[36] Paulsen, V. I., Completely Bounded Maps and Dilations. Pitman Research Notes in Mathematics Series 146, Longman, Scientific & Technical, Harlow, 1986.Google Scholar
[37] Pirkovskii, A., Biprojectivity and biflatness for convolution algebras of nuclear operators. Canad. Math. Bull. 47(2004), no. 3, 445–455.Google Scholar
[38] Revuz, D., Markov Chains. Second edition. North Holland Mathematical Library 11, North Holland Publishing, Amsterdam, 1984.Google Scholar
[39] Rosenblatt, J., Ergodic and mixing random walks on locally compact groups. Math. Ann 257(1981), no. 1, 31–42.Google Scholar
[40] Rosenblatt, M., Markov Processes: Structure and Asymptotic Behaviour. Die Grundlehren der Mathematischen Wissenschaften 184. Springer-Verlag, New York, 1971.Google Scholar
[41] Stratila, S., Modular Theory in Operator Algebras. Abacus Press, Tunbridge Wells, 1981.Google Scholar
[42] Varadarajan, V. S., Groups of automorphisms of Borel spaces. Trans. Amer. Math. Soc. 109(1963), 191–220.Google Scholar
[43] Willis, G., Probability measures on groups and some related ideals in group algebras. J. Funct. Anal. 92(1990), no. 1, 202–263.Google Scholar
[44] Willis, G., Factorization in finite-codimensional ideals in group algebras. Proc. London Math. Soc. 82(2001), no. 3, 676–700.Google Scholar
[45] Zimmer, R. J., Amenable ergodic group actions and an application to Poisson boundaries of random walks. J. Funct. Anal. 27(1978), no. 3, 350–372.Google Scholar
[46] Zimmer, R. J., Ergodic Theory and Semisimple Lie Groups. Monographs in Mathematics 81. Birkhäuser Verlag, Basel, 1984.Google Scholar