Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T09:19:37.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizing the Absolute Continuity of the Convolution of Orbital Measures in aClassical Lie Algebra

Published online by Cambridge University Press:  20 November 2018

Sanjiv Kumar Gupta  and
Kathryn Hare
Sanjiv Kumar Gupta
Affiliation:
Dept. of Mathematics and Statistics, Sultan Qaboos University, P.O. Box 36 Al Khodh 123, Sultanate of Oman e-mail: [email protected]
Kathryn Hare
Affiliation:
Dept. of Pure Mathematics, University of Waterloo, Waterloo ON, N2L 3G1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 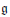$\mathfrak{g}$ be a compact simple Lie algebra of dimension 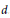$d$. It is a classical result that the convolution of any 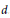$d$ non-trivial, 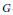$G$-invariant, orbital measures is absolutely continuous with respect to Lebesgue measure on 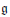$\mathfrak{g}$, and the sum of any 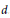$d$ non-trivial orbits has non-empty interior. The number 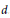$d$ was later reduced to the rank of the Lie algebra (or rank +1 in the case of type 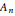${{A}_{n}}$). More recently, the minimal integer 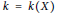$k\,=\,k\left( X \right)$ such that the 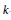$k$-fold convolution of the orbital measure supported on the orbit generated by 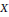$X$ is an absolutely continuous measure was calculated for each 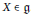$X\,\in \,\mathfrak{g}$.

In this paper 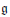$\mathfrak{g}$ is any of the classical, compact, simple Lie algebras. We characterize the tuples 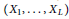$\left( {{X}_{1}},\,.\,.\,.\,,\,{{X}_{L}} \right)$, with 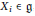${{X}_{i}}\,\in \,\mathfrak{g}$, which have the property that the convolution of the 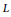$L$-orbital measures supported on the orbits generated by the 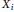${{X}_{i}}$ is absolutely continuous, and, equivalently, the sum of their orbits has non-empty interior. The characterization depends on the Lie type of 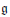$\mathfrak{g}$ and the structure of the annihilating roots of the 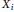${{X}_{i}}$. Such a characterization was previously known only for type 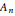${{A}_{n}}$.

Keywords

43A8017B4558C35compact Lie algebraorbital measureabsolutely continuous measure
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 4 , 01 August 2016 , pp. 841 - 875
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Dooley, A. H., Repka, J., and Wildberger, N. J., Sums of adjoint orbits. Linear and Multilinear Algebra 36(1993), no. 2, 79–101.http://dx.doi.org/10.1080/03081089308818278 Google Scholar
[2] Frumkin, A. and Goldberger, A., On the distribution of the spectrum of the sum of two Hermitian or real symmetric spaces. Adv. in Appl. Math. 37(2006), no. 2, 268–286.http://dx.doi.Org/10.1016/j.aam.2005.12.007 Google Scholar
[3] Gratczyk, P. and Sawyer, P., On the kernel of the product formula on symmetric spaces. J. Geom.Anal. 14(2004), no. 4, 653–672.http://dx.doi.org/10.1007/BF02922174 Google Scholar
[4] Gratczyk, P., Absolute continuity of convolutions of orbital measures on Riemannian symmetric spaces. J. Func. Anal. 259(2010), no. 7, 1759–1770.http://dx.doi.Org/10.1016/j.jfa.2010.05.017 Google Scholar
[5] Gratczyk, P., A sharp criterion for the existence of the density in the product formula on symmetric spaces of Type An . J. Lie Theory 20(2010), no. 4, 751–766.Google Scholar
[6] Gupta, S. K. and Hare, K. E., Singularity of orbits in classical Lie algebras. Geom. Func. Anal. 13(2003), 815–844. http://dx.doi.org/10.1007/s00039-003-0431-x Google Scholar
[7] Gupta, S. K., Convolutions of generic orbital measures in compact symmetric spaces. Bull. Aust. Math.Soc. 79(2009), no. 3, 513–522.http://dx.doi.org/10.1017/S0004972709000148 Google Scholar
[8] Gupta, S. K., L2-singular dichotomy for orbital measures of classical compact Lie groups. Adv. Math. 222(2009), no. 5, 1521–1573.http://dx.doi.Org/10.1016/j.aim.2009.06.008 Google Scholar
[9] Gupta, S. K., Hare, K. E., and Seyfaddini, S., L2 -singular dichotomy for orbital measures of classical simple Lie algebras. Math. Z. 262(2009), no. 1, 91–124.http://dx.doi.Org/10.1OO7/sOO2O9-OO8-O364-z Google Scholar
[10] Hare, K. E., Johnstone, D. L., Shi, F., and Yeung, W.-K., L2-singular dichotomy for exceptional Lie groups and algebras. J. Aust. Math. Soc. 95(2013), no. 3, 362–382.http://dx.doi.Org/10.1017/S1446788713000220 Google Scholar
[11] Helgason, S., Differential geometry, Lie groups and symmetric spaces. Pure and Applied Mathematics, 80, Academic Press, New York, 1978.Google Scholar
[12] Humphreys, J. E., Introduction to Lie algebras and representation theory. Graduate Texts in Mathematics, 9, Springer-Verlag, New York, 1972.Google Scholar
[13] Lang, S., Differential and Riemannian manifolds. Graduate Texts in Mathematics, 160,Springer-Verlag, New York, 1995.Google Scholar
[14] Knapp, A. W., Lie groups beyond an introduction. Progress in Mathematics, 140, Birkhâuser Boston, Boston, MA, 2002.Google Scholar
[15] Knutson, A. and Tao, T., Honeycombs and sums of Hermitian matrices. Notices Amer. Math. Soc. 48(2001), no. 2, 175–186.Google Scholar
[16] Mimura, M. and Toda, H., Topology of Lie groups. Translations of Mathematical Monographs, 91,Amererican Mathematical Society, Providence, RI, 1991.Google Scholar
[17] Ragozin, D. L., Zonal measure algebras on isotropy irreducible homogeneous spaces. J. Functional Analysis 17(1974), 355–376.http://dx.doi.Org/10.1016/0022-1236(74)90046-9 Google Scholar
[18] Ragozin, D. L., Central measures on compact simple Lie groups. J. Functional Analysis 10(1972), 212–229.http://dx.doi.Org/10.1016/0022-1236(72)90050-X Google Scholar
[19] Ricci, F. and Stein, E. M., Harmonic analysis on nilpotent groups and singular integrals. II. Singularkernels supported on submanifolds. J. Funct. Anal. 78(1988), no. 1, 56–84.http://dx.doi.Org/10.1016/0022-1236(88)90132-2 Google Scholar
[20] Ricci, F., Harmonic analysis on nilpotent groups and singular integrals. III. Fractional integrationalong manifolds. J. Funct. Anal. 86(1989), no. 2, 360–389.http://dx.doi.Org/10.1016/0022-1236(89)90057-8 Google Scholar
[21] Varadarajan, V. S., Lie groups, Lie algebras and their representations. Graduate Texts in Mathematics, 102, Springer-Verlag, New York, 1984.http://dx.doi.Org/10.1007/978-1-4612-1126-6 Google Scholar
[22] Wright, A., Sums of adjoint orbits and L2-singular dichotomy for SU(m). Adv. Math. 227(2011), no. 1,253–266.http://dx.doi.Org/10.1016/j.aim.2011.02.001 Google Scholar