Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T17:48:36.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of Extremals for some Functionals on Convex Bodies

Published online by Cambridge University Press:  20 November 2018

Christos Saroglou
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate equality cases in inequalities for Sylvester-type functionals. Namely, it was proven by Campi, Colesanti, and Gronchi that the quantity

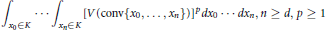$$\int_{{{x}_{0}}\in K}{\cdot \cdot \cdot \int_{{{x}_{n}}\in K}{{{\left[ V\left( \text{conv}\left\{ {{x}_{0}},\cdot \cdot \cdot ,{{x}_{n}} \right\} \right) \right]}^{p}}d{{x}_{0}}\cdot \cdot \cdot }\,d{{x}_{n}},n\ge d,p\ge 1}$$

is maximized by triangles among all planar convex bodies 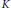$K$ (parallelograms in the symmetric case). We show that these are the only maximizers, a fact proven by Giannopoulos for 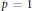$p\,=\,1$. Moreover, if 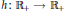$h:\,{{R}_{+}}\,\to \,{{R}_{+}}$ is a strictly increasing function and 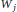[{{W}_{j}}$ is the 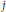$j$-th quermassintegral in 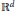${{R}^{d}}$, we prove that the functional

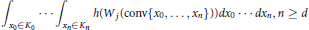$$\int_{{{x}_{0}}\in {{K}_{0}}}{\cdot \cdot \cdot }\int_{{{x}_{n}}\in {{K}_{n}}}{h\left( {{W}_{j}}\left( \text{conv}\left\{ {{x}_{0}},\cdot \cdot \cdot ,{{x}_{n}} \right\} \right) \right)}\,d{{x}_{0}}\cdot \cdot \cdot d{{x}_{n}},n\ge d$$

is minimized among the 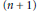$(n\,+\,1)$-tuples of convex bodies of fixed volumes if and only if 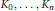${{K}_{0,\,\ldots \,,}}{{K}_{n}}$ are homothetic ellipsoids when 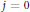$j\,=\,0$ (extending a result of Groemer) and Euclidean balls with the same center when 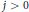$j\,>\,0$ (extending a result of Hartzoulaki and Paouris).

Keywords

52A4052A22
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 6 , 14 December 2010 , pp. 1404 - 1418
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Blaschke, W., Über affine Geometrie XI: Lösung des “Vierpunktproblems” von Sylvester aus der Theorie der geometrischen Wahrscheinlichkeiten. Leipziger Berichte 69(1917), 436–453.Google Scholar
[2] Blaschke, W., Kreis und Kugel. 2te Aufl.,Walter de Gruyter, Berlin, 1956.Google Scholar
[3] Bourgain, J., Meyer, M., Milman, V., and Pajor, A., On a geometric inequality. In: Geometric aspects of functional analysis, Lecture Notes in Math., 1317, Springer, Berlin, 1988, pp. 271–282.Google Scholar
[4] Busemann, H., Volume in terms of concurrent cross-sections. Pacific J. Math. 3(1953), 1–12.Google Scholar
[5] Campi, S., Colesanti, A., and Gronchi, P., A note on Sylvester's problem for random polytopes in a convex body. Rend. Istit. Mat. Univ. Trieste 31(1999), no. 1–2, 79–94.Google Scholar
[6] Campi, S. and Gronchi, P., Extremal convex sets for Sylvester-Busemann type functionals. Appl. Anal. 85(2006), no. 1–3, 129–141. doi:10.1080/00036810500277579Google Scholar
[7] Campi, S. and Gronchi, P., On the reverse Lp-Busemann-Petty centroid inequality. Mathematika 49(2002), no. 1–2, 1–11. doi:10.1112/S0025579300016004Google Scholar
[8] Campi, S. and Gronchi, P., On volume product inequalities for convex sets. Proc. Amer. Math. Soc. 134(2006), no. 8, 2393–2402. doi:10.1090/S0002-9939-06-08241-4Google Scholar
[9] Dalla, L. and Larman, D. G., Volumes of a random polytope in a convex set. In: Applied geometry and discrete mathematics, Ser. Discrete Math. Theoret. Comput. Sci., 4, American Mathematical Society, Providence, RI, 1991, pp. 175–180.Google Scholar
[10] Ewald, G., Larman, D. G., and Rogers, C. A., The directions of the line segments and of the r-dimensional balls on the boundary of a convex body in Euclidean space. Mathematika 17(1970), 1–20. doi:10.1112/S0025579300002655Google Scholar
[11] Gardner, R. J., Geometric tomography. Encyclopedia of Mathematics and its Applications, 58, Cambridge University Press, Cambridge, 1995.Google Scholar
[12] Giannopoulos, A. A., On the mean value of the area of a random polygon in a plane convex body. Mathematika 39(1992), no. 2, 279–290. doi:10.1112/S0025579300015023Google Scholar
[13] Giannopoulos, A. A. and Tsolomitis, A., Volume radius of a random polytope in a convex body. Math. Proc. Cambridge Philos. Soc. 134(2003), no. 1, 13–21. doi:10.1017/S0305004102006254Google Scholar
[14] Groemer, H., On some mean values associated with a randomly selected simplex in a convex set. Pacific J. Math. 45(1973), 525–533.Google Scholar
[15] Groemer, H., On the mean value of the volume of a random polytope in a convex set. Arch. Math. 25(1974), 86–90.Google Scholar
[16] Hartzoulaki, M. and Paouris, G., Quermassintegrals of a random polytope in a convex body. Arch. Math. 80(2003), no. 4, 430–438.Google Scholar
[17] Rogers, C. A. and Shephard, G. C., Some extremal problems for convex bodies. Mathematika 5(1958), 93–102. doi:10.1112/S0025579300001418Google Scholar
[18] Schneider, R., Convex bodies: the Brunn-Minkowski theory. Encyclopedia of Mathematics and its Applications, 44, Cambridge University Press, Cambridge, 1993.Google Scholar
[19] Schöpf, P., Gewichtete Volumsmittelwerte von Simplices, welche zufällig in einem konvexen Körper der Rn gewählt werden. Monatsh. Math. 83(1977), no. 4, 331–337. doi:10.1007/BF01387909Google Scholar
[20] Shephard, G. C., Shadow systems of convex sets. Israel J. Math. 2(1964), 229–236. doi:10.1007/BF02759738Google Scholar