Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T13:18:05.444Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of the Quantum Cohomology Ring of G/B and Applications

Published online by Cambridge University Press:  20 November 2018

Augustin-Liviu Mare
Augustin-Liviu Mare*
Affiliation:
Department of Mathematics and Statistics, University of Regina, Regina, SK, S4S 0A2 e-mail:[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We observe that the small quantum product of the generalized flag manifold 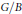$G/B$ is a product operation $\star $ on 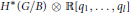${{H}^{*}}(G/B)\otimes \mathbb{R}\left[ {{q}_{1,...,}}{{q}_{l}} \right]$ uniquely determined by the facts that it is a deformation of the cup product on 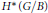${{H}^{*}}(G/B)$; it is commutative, associative, and graded with respect to deg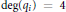$({{q}_{i}})=4$; it satisfies a certain relation (of degree two); and the corresponding Dubrovin connection is flat. Previously, we proved that these properties alone imply the presentation of the ring 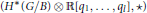$({{H}^{*}}(G/B)\otimes \mathbb{R}\left[ {{q}_{1,...,}}{{q}_{l}} \right]\star )$ in terms of generators and relations. In this paper we use the above observations to give conceptually new proofs of other fundamental results of the quantum Schubert calculus for 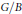$G/B$: the quantum Chevalley formula of D. Peterson (see also Fulton and Woodward) and the “quantization by standard monomials” formula of Fomin, Gelfand, and Postnikov for 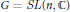$G=SL(n,\mathbb{C})$. The main idea of the proofs is the same as in Amarzaya–Guest: from the quantum 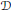$\mathcal{D}$-module of 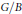$G/B$ one can decode all information about the quantum cohomology of this space.

Keywords

14M1514N35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 4 , 01 August 2008 , pp. 875 - 891
Copyright
Copyright © Canadian Mathematical Society 2008

References

[AG] Amarzaya, A. and Guest, M. A., Gromov-Witten invariants of flag manifolds, via D-modules. J. LondonMath. Soc. 72(2005), no. 1, 121–136.Google Scholar
[BGG] Bernstein, I. N., Gelfand, I. M., and Gelfand, S. I., Schubert cells and cohomology of the space G /P. Uspehi Mat. Nauk 28(1973), no. 3(171), 3–26. (Russian) [Bo] A. Borel, Sur la cohomologie des espaces fibrés principaux et des espaces homogènes des groupes de Lie compacts, Ann. of Math. 57(1953), 115–207.Google Scholar
[Ci] Ciocan-Fontanine, I., The quantum cohomology ring of flag varieties. Trans. Amer.Math. Soc. 351(1999), no. 7, 2695–2729.Google Scholar
[Du] Dubrovin, B., Geometry of 2D topological field theories. In: Integrable Systems and Quantum Groups, Lecture Notes in Mathematics 1620, Springer-Verlag, New York, 1996, 120–348.Google Scholar
[FGP] Fomin, S., Gelfand, S., and A. Postnikov, Quantum Schubert polynomials. J. Amer.Math. Soc. 10(1997), 565–596.Google Scholar
[FP] Fulton, W. and Pandharipande, R., Notes on stable maps and quantum cohomology. In: Algebraic Geometry. Proc. Sympos. Pure Math. 62, Part 2, American Mathematics Society, Providence, RI, 1997, pp. 45–96.Google Scholar
[FW] Fulton, W. and Woodward, C., On the quantum product of Schubert classes. J. Algebraic Geom. 13(2004), no. 4, 641–661.Google Scholar
[Gu] Guest, M. A., Quantum cohomology via D-modules. Topology 44(2005), no. 2, 263–281.Google Scholar
[Ir] Iritani, H., Quantum D-module and equivariant Floer theory for free loop spaces. Math. Z. 252(2006), no. 3, 577–622.Google Scholar
[Ki] Kim, B., Quantum cohomology of flag manifolds G /B and quantum Toda lattices. Ann. of Math. 149(1999), no. 1, 129–148.Google Scholar
[KJ] Kim, B. and Joe, D., Equivariant mirrors and the Virasoro conjecture for flag manifolds. Int.Math. Res. Not. 2003, no. 15 859–882.Google Scholar
[Ma1] Mare, A.-L., On the theorem of Kim concerning QH_(G/B). In: Integrable Systems, Topology and Physics, Contemp.Math. 309, American Mathematical Society, Providence, RI, pp. 151–163.Google Scholar
[Ma2] Mare, A.-L., Polynomial representatives of Schubert classes in QH_(G/B). Math. Res. Lett. 9(2002), no. 5-6, 757–769.Google Scholar
[Ma3] Mare, A.-L., Relations in the quantum cohomology ring of G /B. Math. Res. Lett. 11(2004), no. 1, 35–48.Google Scholar
[Ma4] Mare, A.-L., The combinatorial quantum cohomology ring of G /B. J. Algebraic Combin. 21(2005), no. 3, 331–349.Google Scholar
[ST] Siebert, B. and Tian, G., On quantum cohomology rings of Fano manifolds and a formula of Vafa and Intriligator. Asian J. Math. 1(1997), no. 4, 679–695.Google Scholar